o: \(\dfrac{1}{15}+\dfrac{1}{35}+\dfrac{1}{63}+\dfrac{1}{99}+\dfrac{1}{143}\)
\(=\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+\dfrac{1}{7\cdot9}+\dfrac{1}{9\cdot11}+\dfrac{1}{11\cdot13}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+\dfrac{2}{9\cdot11}+\dfrac{2}{11\cdot13}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{11}-\dfrac{1}{13}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{13}\right)=\dfrac{1}{2}\cdot\dfrac{10}{39}=\dfrac{5}{39}\)
p: \(\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{1\cdot4}+\dfrac{2}{4\cdot7}+\dfrac{2}{7\cdot10}+\dfrac{2}{10\cdot13}+\dfrac{2}{13\cdot16}+\dfrac{2}{16\cdot19}\)
\(=\dfrac{2}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+...+\dfrac{3}{16\cdot19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{19}\right)=\dfrac{2}{3}\cdot\dfrac{18}{19}=\dfrac{2\cdot6}{19}=\dfrac{12}{19}\)
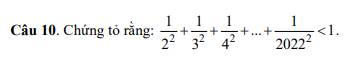
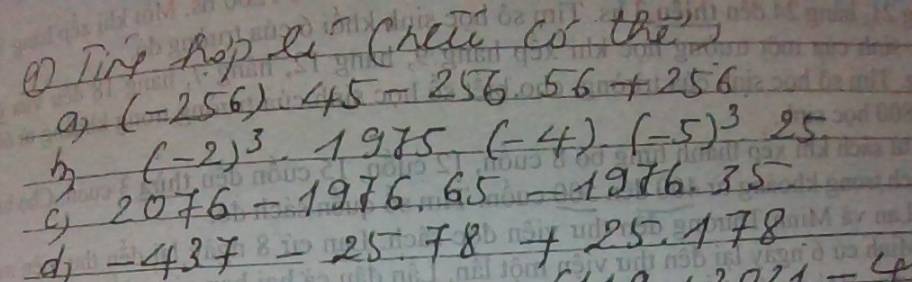cần giúp gấp vs ạ, em cảm ơn nhìu
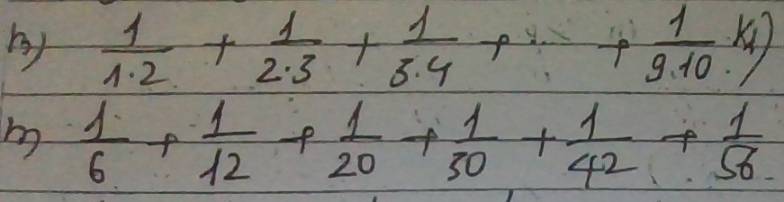giúp em gấp phần m,n với ah cj ơi. Em cám ơn rấc nhìu ạa
