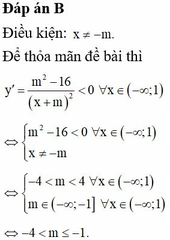Các câu hỏi tương tự
Tập hợp tất cả các giá trị thực của tham số m để hàm số
y
-
x
3
-
6
x
2
+
(
4
m
-
9
)
x
+
4
nghịch biến trên khoảng
-
∞
;
-
1
là A.
(
-
∞
;...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = - x 3 - 6 x 2 + ( 4 m - 9 ) x + 4 nghịch biến trên khoảng - ∞ ; - 1 là
A. ( - ∞ ; 0 ]
B. [ - 3 4 ; + ∞ )
C. ( - ∞ ; - 3 4 ]
D. [ 0 ; + ∞ )
Gọi S là tập hợp các giá trị nguyên của tham số m sao cho hàm số
y
x
-
1
x
-
m
nghịch biến trên khoảng
4
;
+
∞
. Tính tổng P của các giá trị m của S. A.
P
10
B.
P
9
C. ...
Đọc tiếp
Gọi S là tập hợp các giá trị nguyên của tham số m sao cho hàm số y = x - 1 x - m nghịch biến trên khoảng 4 ; + ∞ . Tính tổng P của các giá trị m của S.
A. P = 10
B. P = 9
C. P = - 9
D. P = - 10
Tập hợp tất cả các giá trị thực của tham số m để hàm số
y
-
x
3
-
6
x
2
+
4
m
-
9
x
+
4
nghịch biến trên khoảng (-¥ -; 1) là A.
(
-
∞
;
0
]
B.
[
-...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = - x 3 - 6 x 2 + 4 m - 9 x + 4 nghịch biến trên khoảng (-¥ -; 1) là
A. ( - ∞ ; 0 ]
B. [ - 3 4 ; + ∞ )
C. ( - ∞ ; - 3 4 ]
D. [ 0 ; + ∞ )
Cho hàm số f(x)3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
mf
2
(
x
)
+
3
(
m...
Đọc tiếp
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Tìm các giá trị của tham số m để hàm số
y
1
2
ln
(
x
2
+
4
)
-
m
x
+
3
nghịch biến trên khoảng
(
-
∞
;
+
∞
)
. A.
m
≥
4
B.
m
≤
-
1
4...
Đọc tiếp
Tìm các giá trị của tham số m để hàm số y = 1 2 ln ( x 2 + 4 ) - m x + 3 nghịch biến trên khoảng ( - ∞ ; + ∞ ) .
A. m ≥ 4
B. m ≤ - 1 4
C. m ≥ 1 4
D. m ≤ 4
Số các giá trị nguyên của tham
M
∈
-
2019
;
2019
để hàm số
y
m
+
1
x
2
-
2
m
x
+
6
m...
Đọc tiếp
Số các giá trị nguyên của tham M ∈ - 2019 ; 2019 để hàm số y = m + 1 x 2 - 2 m x + 6 m x - 1 đồng biến trên khoảng 4 ; + ∞ ?
A. 2034
B. 2018
C. 2025
D. 2021
Số các giá trị nguyên của tham
M
∈
[
-
2019
;
2019
]
để hàm số
y
m
+
1
x
2
-
2
m
x
+
6
m...
Đọc tiếp
Số các giá trị nguyên của tham M ∈ [ - 2019 ; 2019 ] để hàm số y = m + 1 x 2 - 2 m x + 6 m x - 1 đồng biến trên khoảng 4 ; + ∞ ?
A. 2034
B. 2018
C. 2025
D. 2021
Các giá trị của tham số m để hàm số
y
mx
+
16
x
+
m
nghịch biến trên khoảng
−
∞
;
1
là A.
m
≥
−
1
B.
-
4
m
≤
−
1
C. ...
Đọc tiếp
Các giá trị của tham số m để hàm số y = mx + 16 x + m nghịch biến trên khoảng − ∞ ; 1 là
A. m ≥ − 1
B. - 4 < m ≤ − 1
C. - 4 ≤ m ≤ 4
D. - 4 < m < 4
Tìm tất cả các giá trị tham số m để hàm số
y
-
1
3
x
3
+
(
m
-
1
)
x
2
+
(
m
+
3
)
x
-
4
đồng biến trên (0;3) A.
m
≥
1
7
B.
m
≥
4
7...
Đọc tiếp
Tìm tất cả các giá trị tham số m để hàm số y = - 1 3 x 3 + ( m - 1 ) x 2 + ( m + 3 ) x - 4 đồng biến trên (0;3)
A. m ≥ 1 7
B. m ≥ 4 7
C. m ≥ 8 7
D. m ≥ 12 7