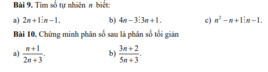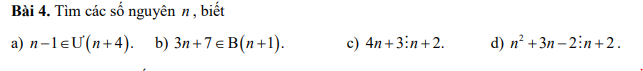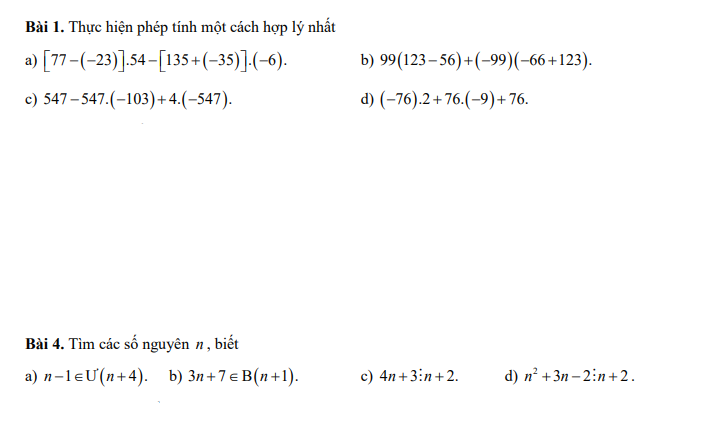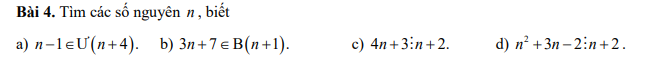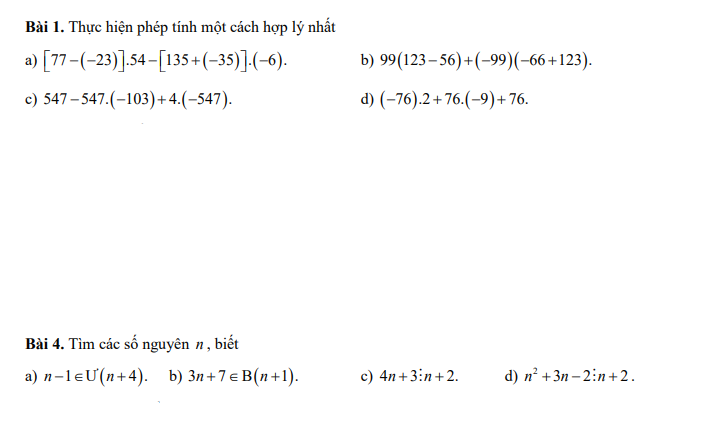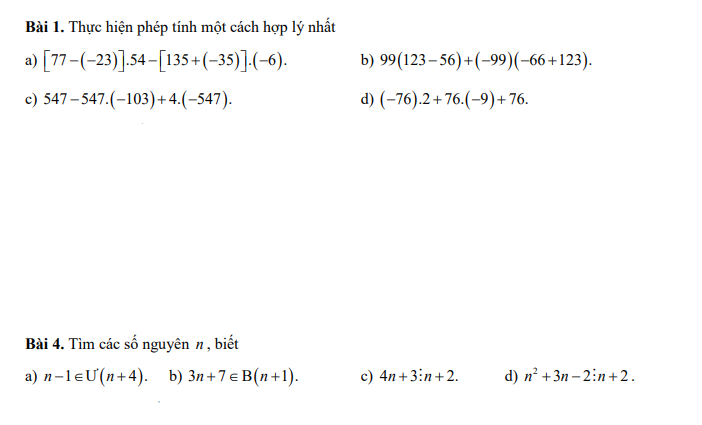Question

Các bạn trình bày đầy đủ và nhanh nhất thì mik like nhé :))

Answer 1

Bài 9:
\(a,\left(2n+1\right)⋮\left(n-1\right)\\ \Rightarrow\left[\left(2n-2\right)+3\right]⋮\left(n-1\right)\\ \Rightarrow\left[2\left(n-1\right)+3\right]⋮\left(n-1\right)\)

Mà \(2\left(n-1\right)⋮\left(n-1\right)\Rightarrow3⋮\left(n-1\right)\Rightarrow n-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)

Ta có bảng:

n-1	-3	-1	1	3
n	-2(loại)	0(tm)	2(tm)	4(tm)

Vậy \(n\in\left\{0;2;4\right\}\)

b, c, d bạn làm tương tự nhé

Answer 2

Bài 10:

a: Gọi a=UCLN(n+1;2n+3)

\(\Leftrightarrow2n+3-2\left(n+1\right)⋮a\)

\(\Leftrightarrow1⋮a\)

=>a=1

Vậy: n+1/2n+3 là phân số tối giản

b: Gọi a=UCLN(3n+2;5n+3)

\(\Leftrightarrow5\left(3n+2\right)-3\left(5n+3\right)⋮a\)

\(\Leftrightarrow1⋮a\)

=>a=1

Vậy: 3n+2/5n+3 là phân số tối giản