Các câu hỏi tương tự
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| |
z
¯
+ 2 + 4i| và
z
-
i
z
¯
+
i
là số thuần ảo.
Đọc tiếp
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| z ¯ + 2 + 4i| và z - i z ¯ + i là số thuần ảo.
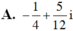
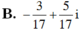

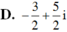
Cho z = a + bi ∈ C, biết 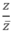 là một số thuần ảo. Kết luận nào sau đây là đúng?
là một số thuần ảo. Kết luận nào sau đây là đúng?
A. a = 0 B. b = 0
C. a = b D. a = b hoặc a = -b
Cho z là một số phức tùy ý. Mệnh đề nào sau đây là sai?A. z
∈
R
⇔
z
z
B. z là thuần ảo
⇔
z +
z
0C.
z
z
-
z
z
∈
R
z...
Đọc tiếp
Cho z là một số phức tùy ý. Mệnh đề nào sau đây là sai?
A. z ∈ R ⇔ z = z
B. z là thuần ảo ⇔ z + z = 0
C. z z = - z z ∈ R z ≠ 0
D. z 3 + z 3 ∈ R
Cho z = a + bi ∈ C, biết z z ¯ là một số thuần ảo. Kết luận nào sau đây là đúng?
A. a = 0 B. b = 0
C. a = b D. a = b hoặc a = -b
Cho số phức z(1-2i)(4-3i)-2+8i. Cho các phát biểu sau: (1) Modun của z là một số nguyên tố (2) z có phần thực và phần ảo đều âm (3) z là số thuần thực (4) Số phức liên hợp của z có phần ảo là 3i Số phát biểu sai là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
A. 1
B. 2
C. 3
D. 4
Cho z
∈
C. Mệnh đề nào sau đây đúng?A. Nếu z
∈
C R thì z là một số thuần ảo.B. Nếu z là một số thuần ảo thì z
∈
C R.C. Nếu z là một số thuần ảo thì z |z|.D. Nếu z là một số thuần ảo thì z
z
Đọc tiếp
Cho z ∈ C. Mệnh đề nào sau đây đúng?
A. Nếu z ∈ C \ R thì z là một số thuần ảo.
B. Nếu z là một số thuần ảo thì z ∈ C \ R.
C. Nếu z là một số thuần ảo thì z = |z|.
D. Nếu z là một số thuần ảo thì z = z
Cho z ∈ C. Mệnh đề nào sau đây đúng?
A. Nếu z ∈ C \ R thì z là một số thuần ảo.
B. Nếu z là một số thuần ảo thì z ∈ C \ R.
C. Nếu z là một số thuần ảo thì z = |z|.
D. Nếu z là một số thuần ảo thì z = z−.
Xét các số phức z thỏa mãn
(
z
+
2
i
)
(
z
¯
+
2
)
là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
Đọc tiếp
Xét các số phức z thỏa mãn ( z + 2 i ) ( z ¯ + 2 ) là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
![]()
![]()
![]()
![]()
Xét các số phức z thỏa mãn là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là A.(1;-1) B.(1;1) C.(-1;1) D.(-1;-1)
Đọc tiếp
Xét các số phức z thỏa mãn ![]() là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
A.(1;-1)
B.(1;1)
C.(-1;1)
D.(-1;-1)




