Đáp án: B.
Gợi ý: Xem lại định nghĩa số thuần ảo, số phức liên hợp và mô đun của số phức.
Đáp án: B.
Gợi ý: Xem lại định nghĩa số thuần ảo, số phức liên hợp và mô đun của số phức.
Cho z ∈ C. Mệnh đề nào sau đây đúng?
A. Nếu z ∈ C \ R thì z là một số thuần ảo.
B. Nếu z là một số thuần ảo thì z ∈ C \ R.
C. Nếu z là một số thuần ảo thì z = |z|.
D. Nếu z là một số thuần ảo thì z = z−.
Cho z ∈ C. Mệnh đề nào sau đây sai?
A. 1 z ∈ R ⇔ z ∈ R
B. 1 z là số thuần ảo ⇔ z là thuần ảo
C. 1 z = z ¯ ⇔ z = 1
D. 1 z = z ⇔ z ∈ R
Cho z là một số phức tùy ý. Mệnh đề nào sau đây là sai?
A. z ∈ R ⇔ z = z
B. z là thuần ảo ⇔ z + z = 0
C. z z = - z z ∈ R z ≠ 0
D. z 3 + z 3 ∈ R
Cho số phức z = a + bi với a , b ∈ R . Nếu z là số thuần ảo thì đâu là khẳng định đúng?
A. a = 0
B. a = 0 và b ≠ 0
C. b = 0
D. b = 0 và a ≠ 0
Cho hai số phức z = - 2 + 5 i , z ' = a + b i ( a , b ∈ R ) Xác định a,b để z + z’ là một số thuần ảo
![]()
![]()
![]()
![]()
Biết z không phải là số phức thuần ảo và M, N là biểu diễn của z và w = - z ¯ thì:
A. M, N đối xứng qua O
B. M N
C. M, N đối xứng nhau qua Ox
D. M, N đối xứng nhau qua Oy
Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
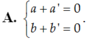
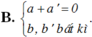
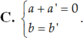
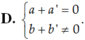
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | z ¯ + 3 + 4i| và z - 2 i z ¯ + i là một số thuần ảo.
![]()
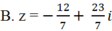
![]()
![]()
Cho z ∈ C. Mệnh đề nào sau đây sai?
A. Nếu z ∈ R thì z = z ¯ .
B. Nếu z = z ¯ thì z ∈ R.
C. Nếu z ∈ R thì z = |z|.
D. Nếu z = |z| thì z ∈ R.