Chọn C.
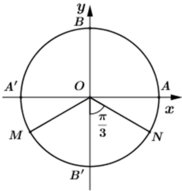
+ Cung α có mút đầu là A và mút cuối là B nên ![]()
OMB’và ONB’ là các tam giác đều nên
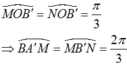
+ Cung α có mút đầu là A và mút cuối là M hoặc N nên
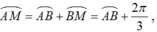
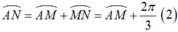
+ Chu kì của cung α là ![]()
Từ (1), (2) ta có 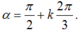
Chọn C.

+ Cung α có mút đầu là A và mút cuối là B nên ![]()
OMB’và ONB’ là các tam giác đều nên
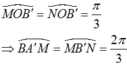
+ Cung α có mút đầu là A và mút cuối là M hoặc N nên
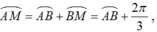
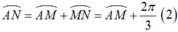
+ Chu kì của cung α là ![]()
Từ (1), (2) ta có 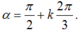
Cho hình vẽ sau. Hỏi cung α có mút đầu là A và mút cuối là M thì số đo của α là
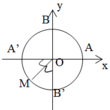
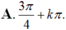
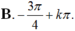
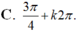
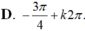
Trên đường tròn đơn vị, gọi các điểm A, B, C, D lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho L, M, N, P lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút trùng với A và có số đo α = - 3 π 4 + k π . Mút cuối của trùng với điểm nào trong các điểm L, M, N, P?
A. L hoặc N
B. M hoặc P
C. M hoặc N
D. L hoặc P
Trên đường tròn đơn vị, gọi các điểm A, B, A’, B’ lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho M, N, P, Q lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút là A và mút cuối trùng với một trong bốn điểm M, N, P, Q. Số do của là
A. α = 300+ k.3600
B. α= 600+ k.3600
![]()
![]()
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo các cung AM1, AM2, AM3.
Góc lượng giác có số đo α (rad) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng :
A. α + k.1800 ( k là số nguyên)
B. α + k. 3600 (k là số nguyên).
C. α + k2π ( k là số nguyên).
D. α + kπ ( k là số nguyên).
Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử ∠AOH = α. Tính AK và OK theo a và α.
Cho cung lượng giác AB có số đo là 15 rad. Tìm số lớn nhất trong các số đo của cung lượng giác điểm đầu A, điểm cuối B, có số đo âm.