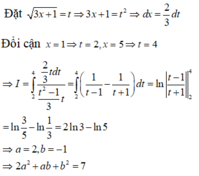Các câu hỏi tương tự
Tính tích phân
I
∫
1
5
1
x
3
x
+
1
d
x
được kết quả I aln3 + bln5 với a, b là các số hữu tỉ. Giá trị của a2 + ab + 3b2 là A. 4. B. -1. C. 0. D. 5.
Đọc tiếp
Tính tích phân I = ∫ 1 5 1 x 3 x + 1 d x được kết quả I = aln3 + bln5 với a, b là các số hữu tỉ. Giá trị của a2 + ab + 3b2 là
A. 4.
B. -1.
C. 0.
D. 5.
Tính tích phân
I
∫
1
5
d
x
x
3
x
+
1
ta được kết quả I aln3 + bln5 Giá trị
S
a
2
+
a
b
+
3
b...
Đọc tiếp
Tính tích phân I = ∫ 1 5 d x x 3 x + 1 ta được kết quả I = aln3 + bln5 Giá trị S = a 2 + a b + 3 b 2 là
A. 0
B. 4
C. 1
D. 5
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + (
y
+
3
)2 + (z + 2)2 72. Mặt phẳng (P): x + by + cz + d 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là: A. b + c + d 2 B. b + c + d 4 C. b + c + d 3 D. b + c + d 1
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + ( y + 3 )2 + (z + 2)2 = 72. Mặt phẳng (P): x + by + cz + d = 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là:
A. b + c + d = 2
B. b + c + d = 4
C. b + c + d = 3
D. b + c + d = 1
Biết\(I=\int\limits^5_2\dfrac{\left|x-2\right|}{x}dx=aln2+bln5+c\) với \(a,b,c\in Z\).Tìm \(a,b,c\)
Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
và
f
(
x
)
1
x
2
+
x
;
f
(
1
)
ln...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x ; f ( 1 ) = ln 1 2 Biết ∫ 1 2 x 2 + 1 f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27/2
B. 1/6
C. 7/6
D. -3/2
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Biết
∫
3
4
d
x
(
x
+
1
)
(
x
-
2
)
a
ln
2
+
b
ln
5
+
c
, với a,b,c là...
Đọc tiếp
Biết ∫ 3 4 d x ( x + 1 ) ( x - 2 ) = a ln 2 + b ln 5 + c , với a,b,c là các số hữu tỉ. Tính S = a - 3b + c
A. S = 3
B. S = 2
C. S = -2
D. S = 4
Kết quả của tích phân
∫
-
1
0
x
+
1
+
2
x
-
1
d
x
được viết dưới dạng a+bln2. Tính giá trị của a+b. A.
3
2...
Đọc tiếp
Kết quả của tích phân ∫ - 1 0 x + 1 + 2 x - 1 d x được viết dưới dạng a+bln2. Tính giá trị của a+b.
A. 3 2
B. - 3 2
C. 5 2
D. - 5 2
Biết kết quả tích phân\(I=\)\(\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}\dfrac{\cos x}{\sin x+1}dx=aln2+bln3\) với \(a,b\) nguyên.Gía trị của \(H=a.b\) là