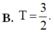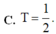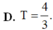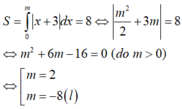Các câu hỏi tương tự
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong
y
x
^
2
+
2
m
x
+
m
2
+
1
, trục hoành, trục tung và đường thẳng x 2. Biết
m
m
0
thì diện tích hình phẳng đó đạt giá trị nhỏ nhất. Giá trị
m
0...
Đọc tiếp
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong y = x ^ 2 + 2 m x + m 2 + 1 , trục hoành, trục tung và đường thẳng x = 2. Biết m = m 0 thì diện tích hình phẳng đó đạt giá trị nhỏ nhất. Giá trị m 0 gần giá trị nào nhất trong các giá trị sau?
A. 0.
B. 1.
C. 4.
D. -3.
Diện tích hình phẳng giới hạn bởi đường cong
y
a
x
(a0), trục hoành và đường thẳng xa bằng
k
a
2
,
(
k
∈
ℝ
)
. Tính giá trị của tham số k.
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y = a x (a>0), trục hoành và đường thẳng x=a bằng k a 2 , ( k ∈ ℝ ) . Tính giá trị của tham số k.
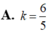
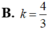
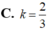
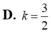
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số
y
-
x
2
+
4
x
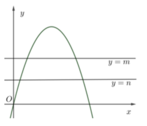
và trục hoành. Hai đường thẳng ym và yn chia thành 3 phần có diện tích bằng nhau (tham khảo hình vẽ). Giá trị biểu thức
T
(
4
-
m
)
3
+...
Đọc tiếp
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = - x 2 + 4 x và trục hoành. Hai đường thẳng y=m và y=n chia thành 3 phần có diện tích bằng nhau (tham khảo hình vẽ). Giá trị biểu thức T = ( 4 - m ) 3 + ( 4 - n ) 3 bằng
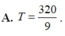
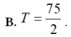
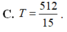
![]()
Gọi (H) là hình phẳng giới hạn bởi parabol (P)
y
8
x
-
x
2
và trục hoành. Các đường thẳng y a; y b;y c với 0abc16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức
16
-
a
3
+
16
-
b...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol (P) y = 8 x - x 2 và trục hoành. Các đường thẳng y = a; y = b;y =c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức 16 - a 3 + 16 - b 3 + 16 - c 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.
Xét hình phẳng (H) được giới hạn bởi các đường thẳng y0, x0 và đường
y
x
+
3
2
. Gọi
A
0
;
9
,
B
b
;
0
−
3
b...
Đọc tiếp
Xét hình phẳng (H) được giới hạn bởi các đường thẳng y=0, x=0 và đường y = x + 3 2 . Gọi A 0 ; 9 , B b ; 0 − 3 < b < 0 . Tìm giá trị của b để đoạn thẳng AB chia (H) thành hai phần có diện tích bằng nhau?
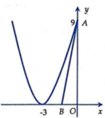
A. b = - 2
B. b = − 1 2
C. b = − 1
D. b = − 3 2
Cho (P)
y
x
2
+
1
và đường thẳng d: mx-y+20. Tìm m để diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất: A. 0,5 B. 0,75 C. 1 D. 0
Đọc tiếp
Cho (P) y = x 2 + 1 và đường thẳng d: mx-y+2=0. Tìm m để diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất:
A. 0,5
B. 0,75
C. 1
D. 0
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
-
6
x
+
9
và 2 đường thẳng x 0; y 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 - 6 x + 9 và 2 đường thẳng x = 0; y = 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
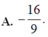
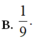
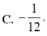
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
x
2
+
1
trục Ox và đường thẳng x1 bằng
a
b
-
ln
1
+
b...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 x 2 + 1 trục Ox và đường thẳng x=1 bằng a b - ln 1 + b c với a,b,c là các nguyên số dương. Khi đó giá trị của a+b+c là:
A. 11.
B. 12.
C. 13.
D. 14.
Xét hình phẳng (H) được giới hạn bởi hàm số
y
x
2
, đường thẳng
y
k
2
với
0
≤
k
≤
1
; trục tung và đường thẳng x1. Biết (H) được chia thành hai phần có diện tích
S
1
S
2
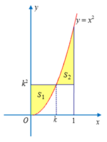
như hình vẽ. Gọi...
Đọc tiếp
Xét hình phẳng (H) được giới hạn bởi hàm số y = x 2 , đường thẳng y = k 2 với 0 ≤ k ≤ 1 ; trục tung và đường thẳng x=1. Biết (H) được chia thành hai phần có diện tích S 1 S 2 như hình vẽ. Gọi k 1 , k 2 lần lượt là giá trị của k làm cho tổng S 1 + S 2 có giá trị lớn nhất và nhỏ nhất. Tính giá trị của T = k 1 + k 2
![]()