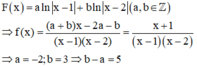Các câu hỏi tương tự
Tìm nguyên hàm của hàm số
f
(
x
)
2008
+
ln
2
x
x
có dạng
F
(
x
)
a
ln
x
+
ln
x
3
b
+
C
. Khi đó tổng S a + b là? A. 2012 B. 2010 C. 2009 D. 2011
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = 2008 + ln 2 x x có
dạng F ( x ) = a ln x + ln x 3 b + C . Khi đó tổng S
= a + b là?
A. 2012
B. 2010
C. 2009
D. 2011
Cho hàm số f (x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
và
f
(
x
)
1
x
2
+
x
,
f
(
1
)
ln
1
2
. Biết...
Đọc tiếp
Cho hàm số f (x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Biết ∫ 1 2 ( x 2 + 1 ) f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27 2
B. 1 6
C. 7 6
D. - 3 2
Cho hàm số
f
x
a
x
+
b
c
x
+
d
với
a
,
b
,
c
,
d
∈
R
có đồ thị hàm số yf(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số yf(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng. A. 2 B. 5 C. 4...
Đọc tiếp
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Biết hàm số
F
(
x
)
a
x
3
+
(
a
+
b
)
x
2
+
(
2
a
-
b
+
c
)
x
+
1
là một nguyên hàm của hàm số
f
(
x
)
3
x
2
+
6...
Đọc tiếp
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Biết
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của hàm số
f
(
x
)
(
2
x
2
-
5
x
+
2
)
e
-...
Đọc tiếp
Biết F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên R. Giá trị của biểu thức f(F(0)) bằng
A. 9e
B. 3e
C. 20 e 2
D. - 1 e
Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
thỏa mãn
f
(
x
)
1
x
2
+
x
,
f
(
1
)
ln
1...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) thỏa mãn f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Cho ∫ 1 2 ( x 2 + 1 ) 2 f ( x ) d x =a ln3+b ln2+c, với a,b,c là các số hữu tỷ. Giá trị biểu thức a+b+c bằng
A. 27 20
B. 23 20
C. - 27 20
D. - 23 20
Kí hiệu F (x) là một nguyên hàm của hàm số
f
(
x
)
1
e
x
+
1
, biết
F
0
-
ln
2
. Tìm tập nghiệm S của phương trình
F
(
x
)
+
ln
(
e
x
+
1
)
3
. A.
S
-...
Đọc tiếp
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Biết F (x) là một nguyên hàm của hàm số
f
(
x
)
10
x
3
-
7
x
+
2
2
x
-
1
thỏa mãn F(1) 5. Giả sử rằng F(3)
a
+
b
5
, trong đó a , b là các số nguyên. Tính tổng bình phương của a và b. A. 121 B. 73 C. 2...
Đọc tiếp
Biết F (x) là một nguyên hàm của hàm số f ( x ) = 10 x 3 - 7 x + 2 2 x - 1 thỏa mãn F(1) = 5. Giả sử rằng F(3) = a + b 5 , trong đó a , b là các số nguyên. Tính tổng bình phương của a và b.
A. 121
B. 73
C. 265
D. 361
Xác định giá trị a, b, c để hàm số
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của
f
(
x
)
(
x
2
-
3
x
+
2
)
e...
Đọc tiếp
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1