Lời giải:
$y_M=\frac{3x_M+4}{x_M-1}$
$\Leftrightarrow 10=\frac{3x_M+4}{x_M-1}$
$\Rightarrow 10(x_M-1)=3x_M+4$
$\Leftrightarrow 7x_M=14$
$\Leftrightarrow x_M=2$
Đáp án B.
Lời giải:
$y_M=\frac{3x_M+4}{x_M-1}$
$\Leftrightarrow 10=\frac{3x_M+4}{x_M-1}$
$\Rightarrow 10(x_M-1)=3x_M+4$
$\Leftrightarrow 7x_M=14$
$\Leftrightarrow x_M=2$
Đáp án B.
Cho hàm số y= x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y= 0 là
A. 1
B. 2
C. 3
D. không có giá trị nào của m thỏa mãn
Cho hàm số y = x - 1 2 x + 1 có đồ thị là (C). Gọi điểm M(x0; y0) với x0 > -1 là điểm thuộc (C) biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB có trọng tâm G nằm trên đường thẳng d: 4x+y=0. Hỏi giá trị của x0+2y0 bằng bao nhiêu?
A . -7/2
B. 7/2
C. 2
D.1
Tọa độ điểm M có hoành độ dương thuộc đồ thị hàm số y = x + 2 x - 2 sao cho tổng khoảng cách từ M đến 2 tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất là
A.![]()
B. ![]()
C.![]()
D.![]()
Cho hàm số y= f(x) =ax3+ bx2+cx+d có đạo hàm là hàm số y= f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
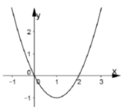
A. 2/3
B. 1
C. 3/2
D. 4/3
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác ∆ O A B cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1.
D. -3.
Tọa độ điểm M có hoành độ nguyên thuộc đồ thị (C) của hàm số y = x + 2 x - 1 có khoảng cách đến đường thẳng
d: x - y +1 = 0 bằng 1 2 là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 1 : Cho hàm số y = x3 - 3m2x2 - m3 có đồ thị (C) . Tìm tất cả các giá trị thực của tham số m để tiếp tuyến của đồ thị (C) tại điểm có hoành độ x0 = 1 song song với đường thẳng d = -3x
A. m = 1
B. m = -1
C.
D. Không có giá trị của m
Câu 2 : Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = x4 - 2x2 + 3 trên [0;2] là:
A. M = 11 , m = 3
B. M = 5 , m = 2
C. M = 3 , m = 2
D. M = 11 , m = 2
Câu 3 : Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng a3 Tính chiều cao h của hình chóp đã cho.
Câu 4 : Hình đa diện nào dưới đây không có tâm đối xứng ?
A. Hình tứ diện đều.
B. Hình lăng trụ tam giác đều.
C. Hình bát diện đều.
D. Hình lập phương.
Câu 5 : Số đường tiệm cận của đồ thị hàm số 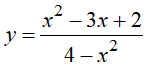
A. 4.
B. 1.
C. 2.
D. 3.
Câu 6 : Cho hàm số 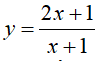
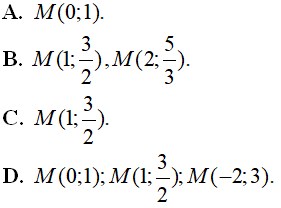
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho đồ thị (C) của hàm số y = x 2 - 3 x x - 1 Hỏi có bao nhiêu điểm thuộc đồ thị (C) có tọa độ nguyên (hoành độ và tung độ là những số nguyên)?
A. 4 điểm
B. Vô số điểm
C. 2 điểm
D. Không có điểm nào