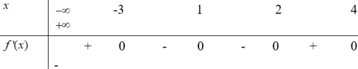Đáp án A
Bất phương trình đã cho ⇔ 1 + 2 x + 1 + x 2 − x + 1 − x 2 + 2 x 3 + 1 < m (*)
Đặt t = x + 1 + x 2 − x + 1
⇔ t 2 = x 2 + 2 + 2 x 3 + 1 ⇔ x 2 + 2 x 3 + 1 = t 2 − 2
Khi đó, bất phương trình * ⇔ 1 + 2 t − t 2 − 2 < m
⇔ m > f t = − t 2 + 2 t + 3 I .
Với x > − 1 suy ra t > 3
khi đó: I ⇔ m ≥ max 3 ; + ∞ f t = 2 3 .