Question

Bài 3. 

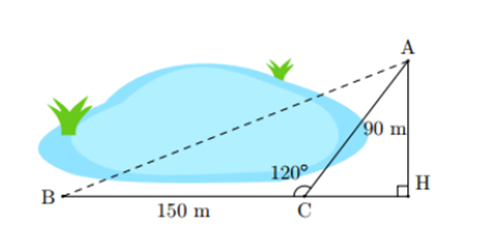
1) Bạn An muốn tính khoảng cách AB (làm tròn đến hàng phần mười của mét) ở hai bên hồ nước (hình vẽ). Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và bạn ấy dùng giác kế đo được $\widehat{ACB}=120°$. Hãy tính AB giúp bạn An.

2) Cho tam giác ABC vuông tại A có đường cao AH (H ∈ BC).

a) Biết AC = 4 cm và $\hat{C}=40°$. Tính độ dài đường cao AH, cạnh AB và BC (làm tròn kết quả đến hàng phần trăm của cm).

b) Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N. Chứng minh rằng ${\tan }^{3}C=\frac{BM}{CN}$.

Answer 1

Bài 2:

a: Xét ΔAHC vuông tại H có \(sinC=\dfrac{AH}{AC}\)

=>\(AH=AC\cdot sin40=4\cdot sin40\simeq2,57\left(cm\right)\)

Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)

=>\(AB=AC\cdot tanC=4\cdot tan40\simeq3,36\left(cm\right)\)

Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)

=>\(BC=\dfrac{AB}{sinC}\simeq3.36:sin40\simeq5,23\left(cm\right)\)

b: Xét ΔBHA vuông tại H có HM là đường cao

nên \(BM\cdot BA=BH^2\)

=>\(BM=\dfrac{BH^2}{BA}\)

Xét ΔCHA vuông tại H có HN là đường cao

nên \(CN\cdot CA=CH^2\)

=>\(CN=\dfrac{CH^2}{CA}\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)

\(\dfrac{BM}{CN}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{AC}=\dfrac{BH^2}{AB}\cdot\dfrac{AC}{CH^2}\)

\(=\left(\dfrac{BH}{CH}\right)^2\cdot\dfrac{AC}{AB}=\left(\dfrac{AB^2}{AC^2}\right)^2\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}=\left(\dfrac{AB}{AC}\right)^3=tan^3C\)