Question

Bài 1:cho tam giác ADF vuông tại D.Kẻ EM là phân giác góc DEF. Trên cạnh EF lấy P sao chk EP = ED.Chứng minh:

A.tam giác DEM  = tam giác PEM

B.PM vuông góc với EF

C.PM  cắt DE tại I. Chứng minh MI = MF

Answer 1

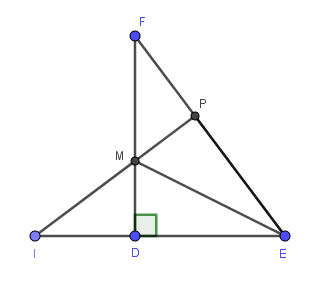
Sửa đề: Tam giác DEF vuông tại D

Giải

a) Do EM là tia phân giác của \(\widehat{DEF}\left(gt\right)\)

\(\Rightarrow\widehat{DEM}=\widehat{FEM}\)

\(\Rightarrow\widehat{DEM}=\widehat{PEM}\)

Xét \(\Delta DEM\) và \(\Delta PEM\) có:

\(EM\) là cạnh chung

\(\widehat{DEM}=\widehat{PEM}\left(cmt\right)\)

\(ED=EP\left(gt\right)\)

\(\Rightarrow\Delta DEM=\Delta PEM\left(c-g-c\right)\)

b) Do \(\Delta DEM=\Delta PEM\left(cmt\right)\)

\(\Rightarrow\widehat{MDE}=\widehat{MPE}\) (hai góc tương ứng)

Mà \(\widehat{MDE}=90^0\)

\(\Rightarrow\widehat{MPE}=90^0\)

\(\Rightarrow PM\perp PE\)

\(\Rightarrow PM\perp EF\)

c) Do \(PM\perp EF\left(cmt\right)\)

\(\Rightarrow\Delta MPF\) vuông tại P

Do \(\Delta DEM=\Delta PEM\left(cmt\right)\)

\(\Rightarrow MD=MP\) (hai cạnh tương ứng)

Xét hai tam giác vuông: \(\Delta MDI\) và \(\Delta MPF\) có:

\(MD=MP\left(cmt\right)\)

\(\widehat{DMI}=\widehat{PMF}\) (đối đỉnh)

\(\Rightarrow\Delta MDI=\Delta MPF\) (cạnh góc vuông - góc nhọn kề)

\(\Rightarrow MI=MP\) (hai cạnh tương ứng)