Bài 19:
b: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔBAC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\)
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
Hình thang BEDC có
M là trung điểm của BE
N là trung điểm của DC
Do đó: MN là đường trung bình của hình thang BEDC
Suy ra: MN//ED//BC và \(MN=\dfrac{ED+BC}{2}\)
hay \(MN=\dfrac{3}{4}BC\)
Xét ΔBED có
M là trung điểm của BE
MP//ED
Do đó: P là trung điểm của BD
Xét ΔCED có
N là trung điểm của DC
QN//ED
Do đó: Q là trung điểm của EC
Xét ΔBED có
M là trung điểm của BE
P là trung điểm của BD
Do đó: MP là đường trung bình của ΔBED
Suy ra: \(MP=\dfrac{ED}{2}=\dfrac{1}{4}BC\left(1\right)\)
Xét ΔCED có
Q là trung điểm của EC
N là trung điểm của DC
Do đó: QN là đường trung bình của ΔCED
Suy ra: \(QN=\dfrac{ED}{2}=\dfrac{1}{4}BC\left(2\right)\)
Ta có: MP+PQ+QN=MN
nên \(PQ=\dfrac{1}{4}BC\left(3\right)\)
Từ (1), (2) và (3) suy ra MP=PQ=QN

 Bài 17,19,20,21
Bài 17,19,20,21 


 Bài 17,19,20,21
Bài 17,19,20,21 Bài 17,19,20,21
Bài 17,19,20,21 Bài 17,19,20,21
Bài 17,19,20,21 Bài 17,19,20,21
Bài 17,19,20,21 bài 17,19,20,21 ạ
bài 17,19,20,21 ạ Bài 17,19,20,21 ạ. e cần gấp
Bài 17,19,20,21 ạ. e cần gấp

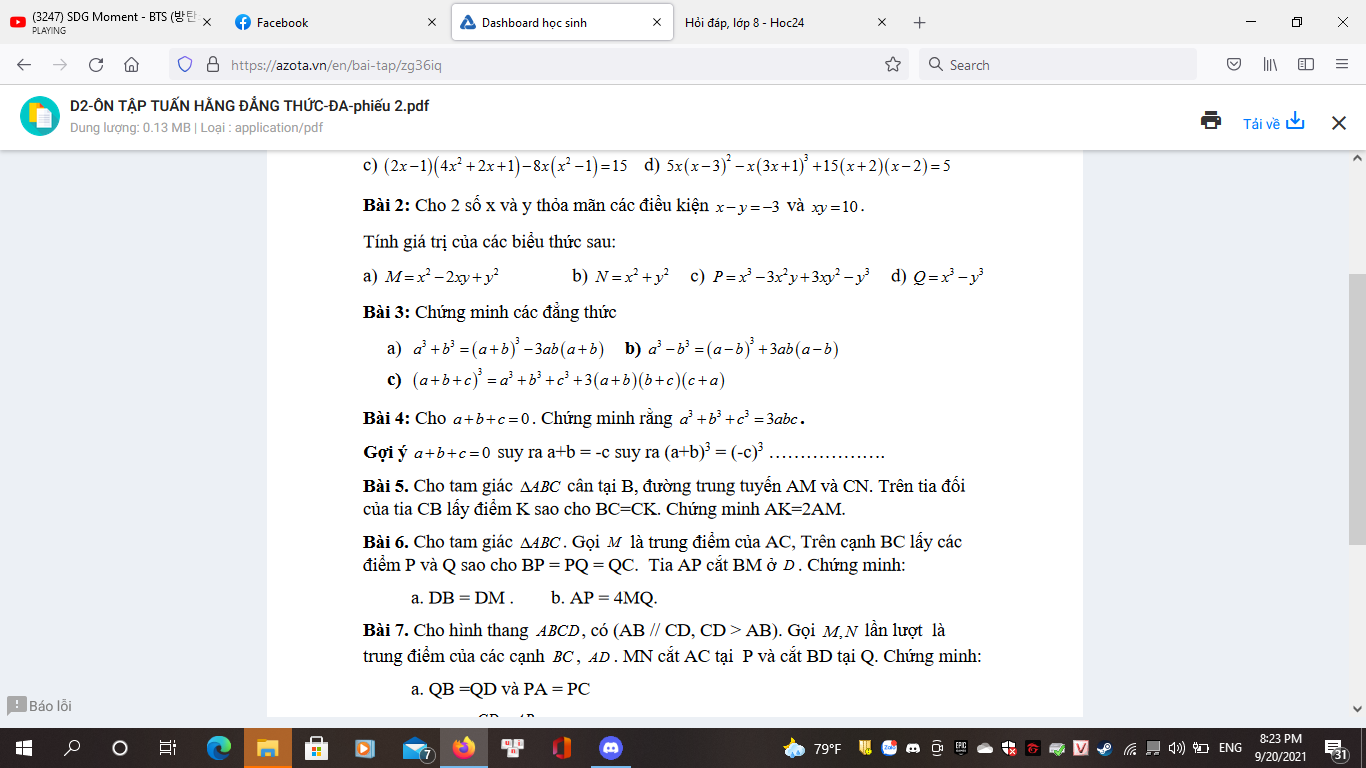 mng giúp mình bài 2 bài 3 bài 4 vs ah
mng giúp mình bài 2 bài 3 bài 4 vs ah