Bài 1. Cho hàm số bậc nhất y = mx + 3.
a) Tìm m để đồ thị hàm số đi qua điểm A2; 1 .
b) Tìm m để đồ thị hàm số song song với đường th ng y = x – 5.
c) Vẽ đồ thị của hàm số với giá trị m tìm được ở câu b.
d) Gọi A , B lần lượt là giao điểm của đồ thị hàm số ở câu c với trục hoành và trục tung. Tính diện
tích của tam giác OAB (đơn vị đo trên các trục toạ độ là centimét)
Bài 1:
a: Thay x=2 và y=1 vào y=mx+3, ta được:
m*2+3=1
=>2m=-2
=>m=-1
b: Để đồ thị hàm số y=mx+3 song song với đường thẳng y=x-5 thì \(\left\{{}\begin{matrix}m=1\\3\ne-5\left(đúng\right)\end{matrix}\right.\)
=>m=1
c: Thay m=1 vào y=mx+3, ta được:
\(y=1\cdot x+3=x+3\)
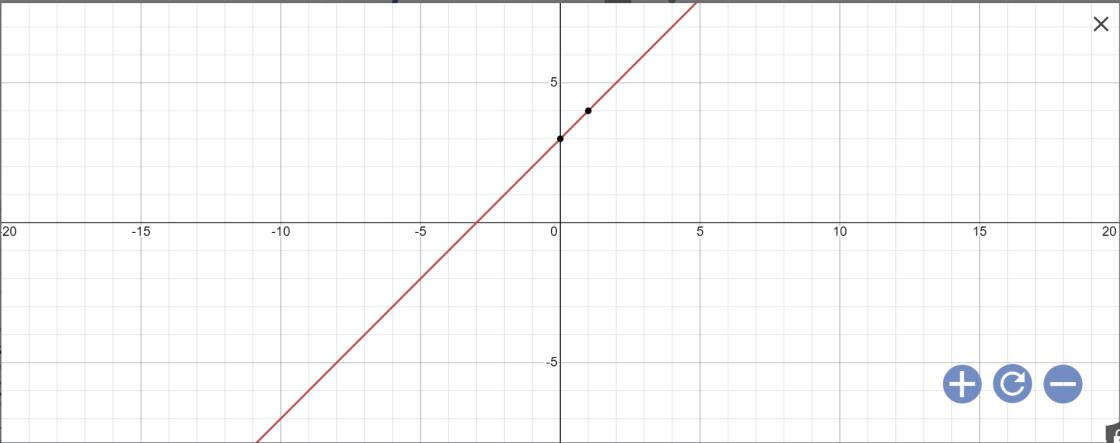
d: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x+3=0+3=3\end{matrix}\right.\)
Vậy: A(-3;0); B(0;3)
\(OA=\sqrt{\left(-3-0\right)^2+\left(0-0\right)^2}=3\)
\(OB=\sqrt{\left(0-0\right)^2+\left(3-0\right)^2}=3\)
Vì ΔOAB vuông tại O
nên \(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=4,5\left(cm^2\right)\)












