B1 : Cho tam giác ABC có AB = AC và M là trung điểm của BC , gọi N là trung điểm của AB , trên tia đối của tia NC lấy điểm K sao cho NK = NC .
a, C/m : Tam giác ABM và tam giác ACM ?
b, C/m : AK = 2.MC
c, Góc MAK = ?
Vẽ hình giúp em với ạ
B2 : Cho tam giác ABC vuông tại A và AB < AC . Trên cạnh BC lấy điểm E sao cho BE = BA , kẻ BD là tia p/g góc ABC ( D thuộc AC ).
a, C/m : Tam giác ABD và tam giác EBD
b, C/m : DE vuông góc BC
c, Gọi K là giao điểm của BA và ED . C/m : BK = BC
Vẽ hình giúp em với ạ
Bài 2
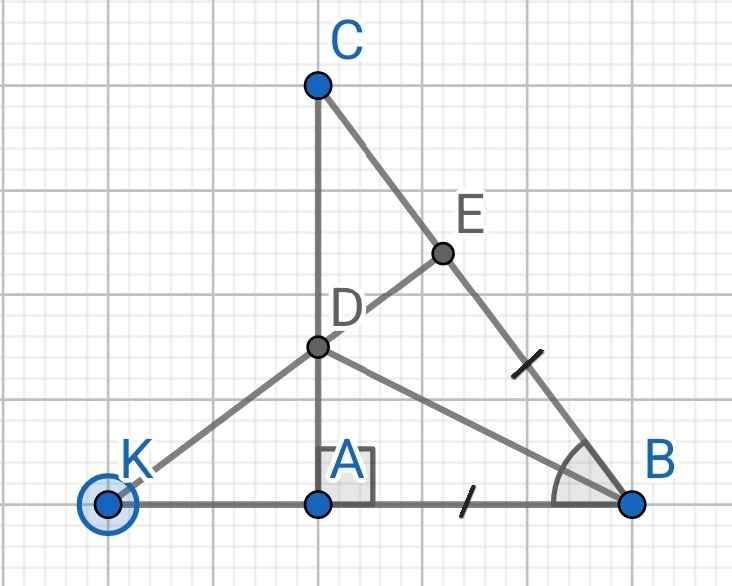
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BE
⇒ DE ⊥ BC
c) Do DE ⊥ BC (cmt)
⇒ ∠DEC = 90⁰
⇒ ∆DEC vuông tại E
Do ∆ABD = ∆EBD (cmt)
⇒ AD = DE (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ADK và ∆DEC có:
AD = DE (cmt)
∠ADK = ∠EDC (đối đỉnh)
⇒ ∆ADK = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AK = EC (hai cạnh tương ứng)
Ta có:
AB = BE (gt)
AK = EC (cmt)
⇒ AB + AK = BE + EC
⇒ BK = BC
Bài 1
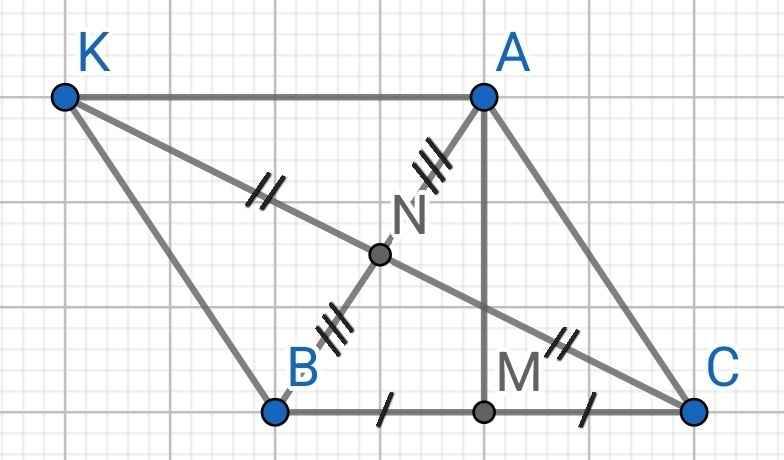 a) Xét ∆ABM và ∆ACM có:
a) Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (gt)
MB = MC (gt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do M là trung điểm của BC
⇒ BC = 2MC
Xét ∆ANK và ∆BNC có:
AN = BN (gt)
NK = NC (gt)
∠ANK = ∠BNC (đối đỉnh)
⇒ ∆ANK = ∆BNC (c-g-c)
⇒ AK = BC (hai cạnh tương ứng)
Mà BC = 2MC (cmt)
⇒ AK = 2MC
c) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
⇒ ∆AMB vuông tại M
⇒ ∠ABM + ∠BAM = 90⁰ (1)
Do ∆ANK = ∆BNC (cmt)
⇒ ∠KAN = ∠NBC (hai góc tương ứng)
⇒ ∠KAN = ∠ABM (2)
Từ (1) và (2) ⇒ ∠MAK = ∠KAN + ∠BAM = 90⁰
Bài 2:
a: Xét ΔABDvà ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}=90^0\)
=>DE\(\perp\)BC
c: Xét ΔBEK vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBK}\) chung
Do đó: ΔBEK=ΔBAC
=>BK=BC














