1: ĐKXĐ: x<>4 và y>=-1
\(\left\{{}\begin{matrix}\dfrac{3}{x-4}+2\sqrt{y+1}=\dfrac{15}{2}\\\dfrac{2}{x-4}-\sqrt{y+1}=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{x-4}+2\sqrt{y+1}=\dfrac{15}{2}\\\dfrac{4}{x-4}-2\sqrt{y+1}=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{7}{x-4}=\dfrac{15}{2}-4=\dfrac{7}{2}\\\dfrac{2}{x-4}-\sqrt{y+1}=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-4=2\\\sqrt{y+1}=\dfrac{2}{2}+2=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-4=2\\y+1=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=6\\y=8\end{matrix}\right.\left(nhận\right)\)
2:
Vì \(\dfrac{m}{1}\ne\dfrac{1}{-m}\)
nên hệ luôn có nghiệm duy nhất
\(\left\{{}\begin{matrix}mx+y=4\\x-my=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}mx+y=4\\x=1+my\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(my+1\right)+y=4\\x=my+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2y+m+y-4=0\\x=my+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y\left(m^2+1\right)=-m+4\\x=my+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{-m+4}{m^2+1}\\x=\dfrac{-m^2+4m}{m^2+1}+1=\dfrac{4m+1}{m^2+1}\end{matrix}\right.\)
Để x và y là hai số đối nhau thì x+y=0
=>-m+4+4m+1=0
=>3m+5=0
=>3m=-5
=>\(m=-\dfrac{5}{3}\)
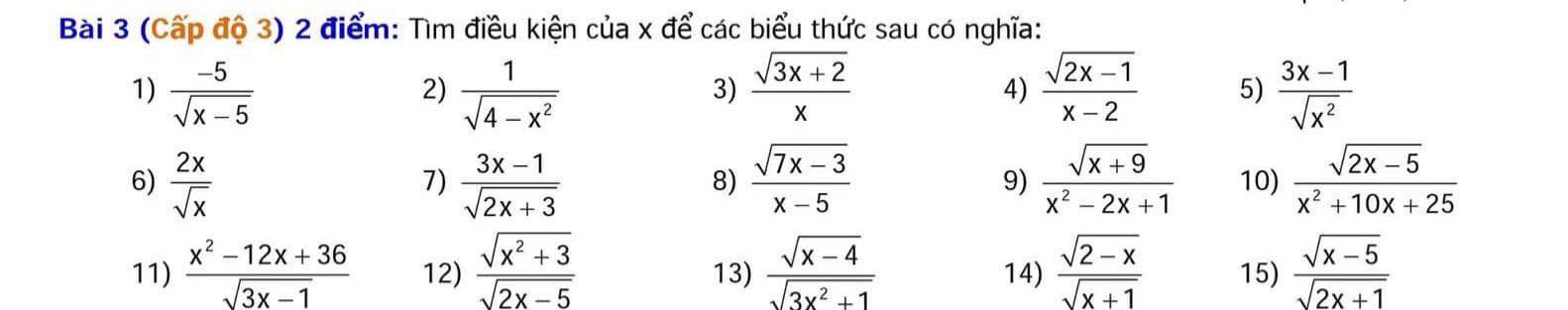
Anh chị giúp em với ạ^^
