Bài 1:
\(a,\widehat{yOz}+\widehat{zOx}=180^0\left(kề.bù\right)\Rightarrow\widehat{yOz}=180^0-50^0=130^0\Rightarrow\widehat{yOz}=\widehat{yOt}\left(=130^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên Oz//Bt
\(b,\left\{{}\begin{matrix}Oz//Bt\\OH\perp Bt\end{matrix}\right.\Rightarrow OH\perp Oz\)
\(c,\) Kẻ phân giác Oa của góc yOz
Suy ra \(\widehat{aOm}=\widehat{aOz}+\widehat{zOm}=\dfrac{1}{2}\widehat{yOz}+\dfrac{1}{2}\widehat{zOx}=\dfrac{1}{2}\left(\widehat{yOz}+\widehat{zOx}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
Do đó Oa⊥Om
Do Oa là p/g góc yOz và On là p/g góc yOt nên \(\left\{{}\begin{matrix}\widehat{yBn}=\dfrac{1}{2}\widehat{yOt}\\\widehat{yOa}=\dfrac{1}{2}\widehat{yOz}\end{matrix}\right.\)
Mà \(\widehat{yOt}=\widehat{yOz}\) nên \(\widehat{yBn}=\widehat{yOa}\) mà 2 góc này ở vị trí đồng vị nên Oa//Bn
Do đó Om⊥Bn












 làm hộ em nhé :>
làm hộ em nhé :>


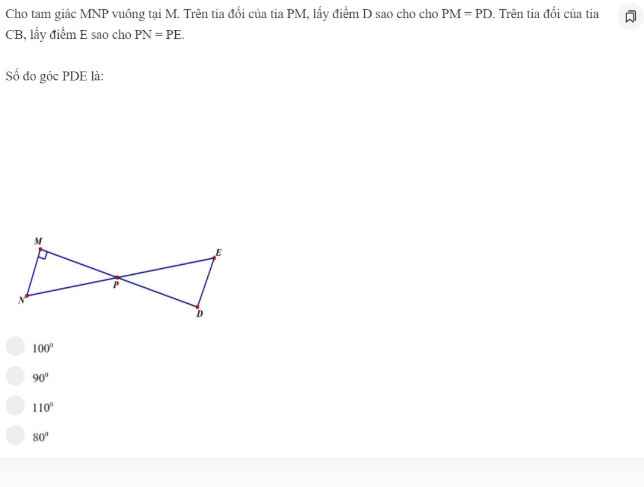 ai làm hộ em với ạ !
ai làm hộ em với ạ ! ai làm hộ em với ạ!
ai làm hộ em với ạ! ai làm hộ em với ạ !
ai làm hộ em với ạ !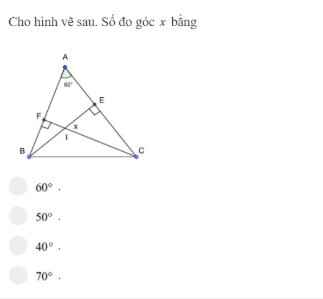 ai làm hộ em với ạ !
ai làm hộ em với ạ !