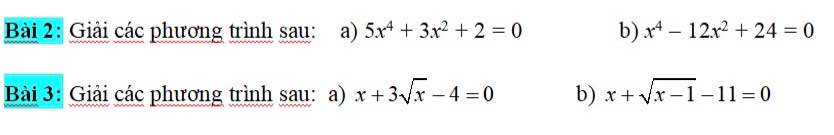Gọi thời gian chảy một mình đầy bể của vòi thứ nhất và vòi thứ hai lần lượt là x(giờ) và y(giờ)
(ĐK: x>0 và y>0)
Trong 1 giờ, vòi thứ nhất chảy được: \(\dfrac{1}{x}\left(bể\right)\)
Trong 1 giờ, vòi thứ hai chảy được: \(\dfrac{1}{y}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được \(\dfrac{1}{5}\left(bể\right)\)
=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\left(1\right)\)
Trong 3 giờ, vòi thứ nhất chảy được: \(\dfrac{3}{x}\left(bể\right)\)
Trong 4 giờ, vòi thứ hai chảy được: \(\dfrac{4}{y}\left(bể\right)\)
Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ hai chảy trong 4 giờ thì hai vòi chảy được 2/3 bể nên ta có: \(\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{2}{3}\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\\\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{4}{5}\\\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{2}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}-\dfrac{3}{x}-\dfrac{4}{y}=\dfrac{4}{5}-\dfrac{2}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{12-10}{15}=\dfrac{2}{15}\\\dfrac{1}{y}=\dfrac{1}{5}-\dfrac{2}{15}=\dfrac{1}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{15}{2}\\y=15\end{matrix}\right.\left(nhận\right)\)
vậy: thời gian chảy một mình đầy bể của vòi thứ nhất và vòi thứ hai lần lượt là 7,5 giờ và 15 giờ






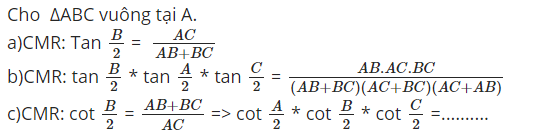

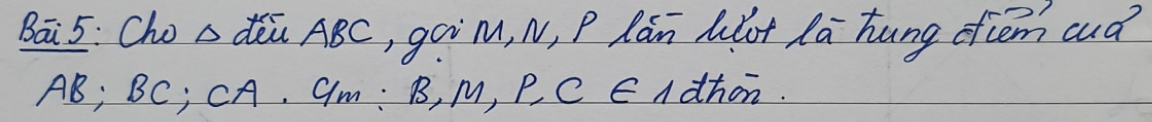






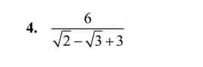
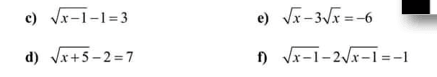


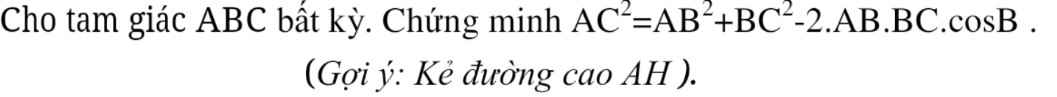




 Ai giúp mk vs ạ 🥲😞
Ai giúp mk vs ạ 🥲😞