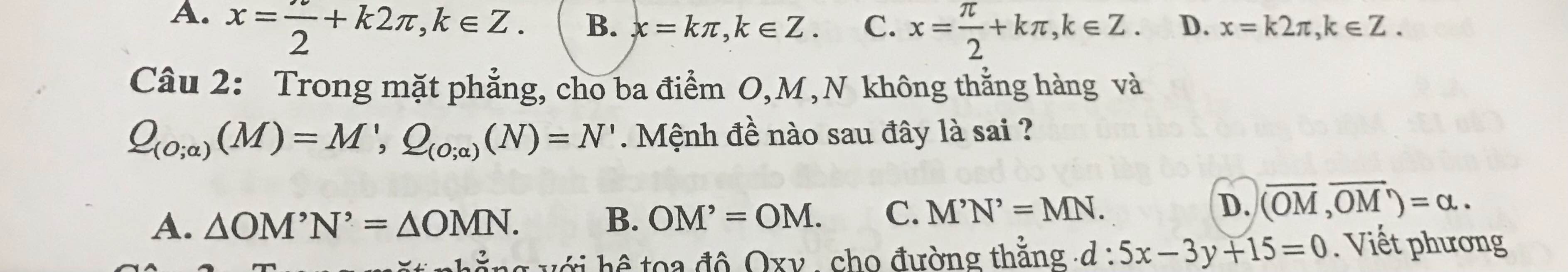Câu 4:
Ta có: \(\left\{{}\begin{matrix}u_5-u_2=78\\u_6-u_3=234\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1.q^4-u_1.q=78\\u_1.q^5-u_1.q^2=234\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1.q\left(q^3-1\right)=78\\u_1.q^2.\left(q^3-1\right)=234\end{matrix}\right.\)
Từ đó ta có: \(\dfrac{u_1.q.\left(q^3-1\right)}{u_1.q^2.\left(q^3-1\right)}=\dfrac{78}{234}\)
\(\Rightarrow\dfrac{1}{q}=\dfrac{1}{3}\)
\(\Rightarrow q=3\). Thay \(u_1.q.\left(q^3-1\right)=78\) ta có:
\(u_1.3.\left(3^3-1\right)=78\)
\(\Rightarrow u_1.78=78\)
\(\Rightarrow u_1=1\)
Vậy số hạng đầu và công bội của cấp số nhân này lần lượt là: \(u_1=1,q=3\)
Câu 4: \(\left\{{}\begin{matrix}u_5-u_2=78\\u_6-u_3=234\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1\cdot q^4-u_1\cdot q=78\\u_1\cdot q^5-u_1\cdot q^2=234\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1\cdot q\left(q^3-1\right)=78\\u_1\cdot q^2\left(q^3-1\right)=234\end{matrix}\right.\)
=>\(\dfrac{u_1\cdot q^2\cdot\left(q^3-1\right)}{u_1\cdot q\left(q^3-1\right)}=\dfrac{234}{78}\)
=>q=3
\(u_1=\dfrac{78}{q\left(q^3-1\right)}=\dfrac{78}{3\left(3^3-1\right)}=\dfrac{26}{26}=1\)
Câu 3: \(\left\{{}\begin{matrix}u_4-u_2=72\\u_5-u_3=144\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_2\cdot q^2-u_2=72\\u_2\cdot q^3-u_2\cdot q=144\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_2\left(q^2-1\right)=72\\u_2\cdot q\cdot\left(q^2-1\right)=144\end{matrix}\right.\)
=>\(\dfrac{u_2\cdot q\left(q^2-1\right)}{u_2\cdot\left(q^2-1\right)}=\dfrac{144}{72}\)
=>q=2
\(u_2=\dfrac{72}{q^2-1}=\dfrac{72}{2^2-1}=\dfrac{72}{4-1}=\dfrac{72}{3}=24\)
\(u_1=\dfrac{u_2}{q}=\dfrac{24}{2}=12\)
Tổng của 8 số hạng đầu tiên là:
\(S_8=\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{12\cdot\left(1-2^8\right)}{1-2}=3060\)










 ai giải giúp em với ạ
ai giải giúp em với ạ