a: Xét tứ giác ABEF có \(\hat{EBF}=\hat{EAF}=90^0\)
nên ABEF là tứ giác nội tiếp
b: ABEF là tứ giác nội tiếp
=>\(\hat{ABE}+\hat{AFE}=180^0\)
mà \(\hat{ABE}+\hat{DBA}=180^0\) (hai góc kề bù)
nên \(\hat{DBA}=\hat{DFE}\)
Xét ΔDBA và ΔDFE có
\(\hat{DBA}=\hat{DFE}\)
góc BDA chung
Do đó: ΔDBA~ΔDFE
=>\(\frac{DB}{DF}=\frac{DA}{DE}\)
=>\(DB\cdot DF=DE\cdot DA\)
c: Xét (O) có \(\hat{EDF}\) là góc nội tiếp chắn cung EF
=>\(\hat{EOF}=2\cdot\hat{EDF}=2\cdot60^0=120^0\)
Xét tứ giác DBHA có \(\hat{DBH}+\hat{DAH}=90^0+90^0=180^0\)
nên DBHA là tứ giác nội tiếp
=>\(\hat{BHA}+\hat{BDA}=180^0\)
=>\(\hat{BHA}=180^0-60^0=120^0\)
mà \(\hat{EHF}=\hat{BHA}\) (hai góc đối đỉnh)
nên \(\hat{EHF}=120^0\)
I là tâm đường tròn nội tiếp ΔDEF
=>EI là phân giác của góc DEF, FI là phân giác của góc DFE
Xét ΔDEF có \(\hat{DEF}+\hat{DFE}+\hat{EDF}=180^0\)
=>\(\hat{DEF}+\hat{DFE}=180^0-60^0=120^0\)
=>\(2\left(\hat{IEF}+\hat{IFE}\right)=120^0\)
=>\(\hat{IEF}+\hat{IFE}=60^0\)
Xét ΔEIF có \(\hat{EIF}+\hat{IEF}+\hat{IFE}=180^0\)
=>\(\hat{EIF}=180^0-60^0=120^0\)
=>\(\hat{EIF}=\hat{EHF}=\hat{EOF}\left(=120^0\right)\)
=>E,I,F,H,O cùng thuộc một đường tròn






 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)


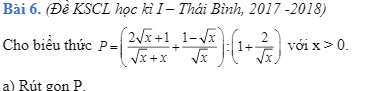


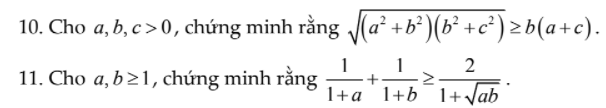



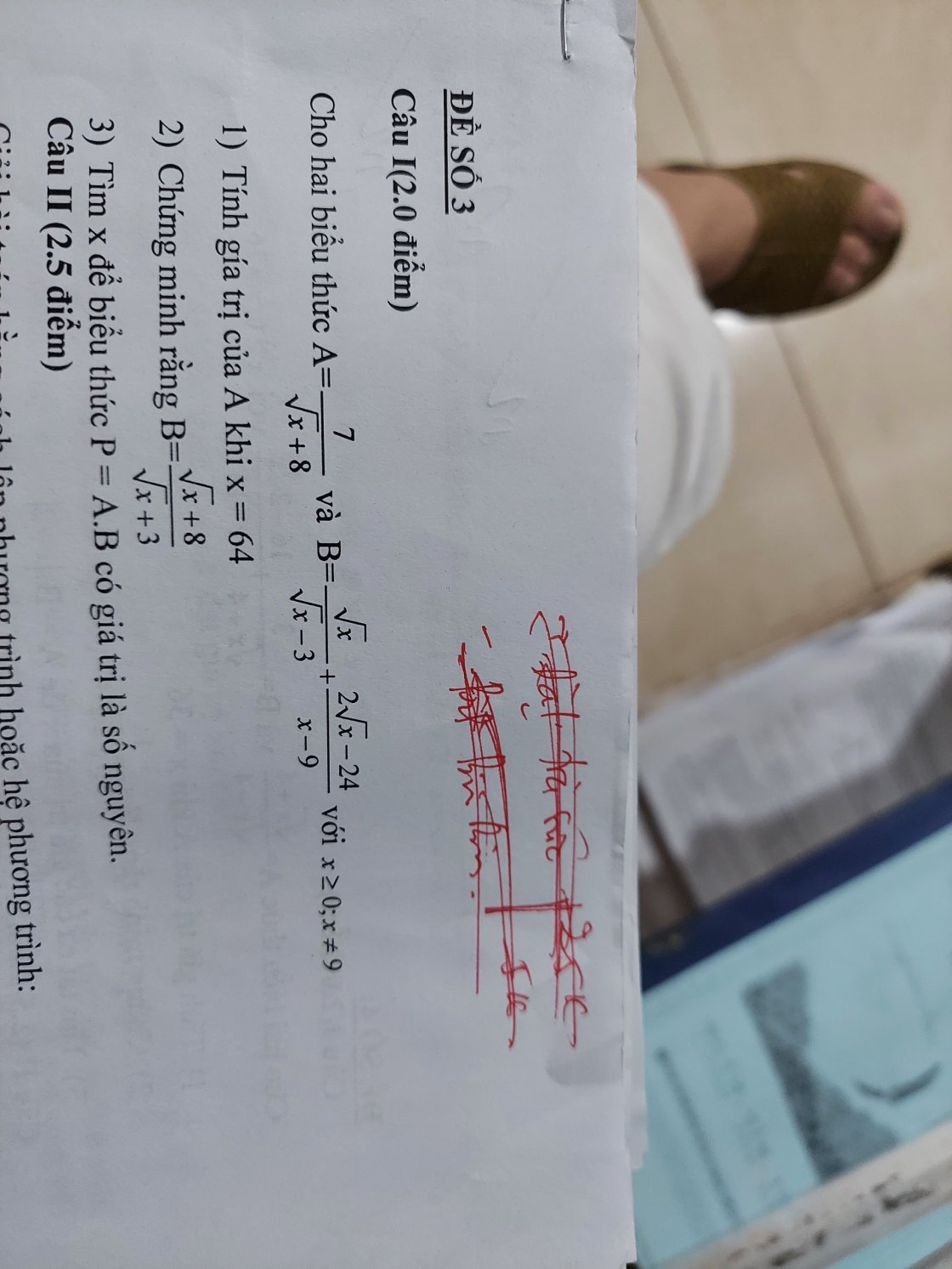

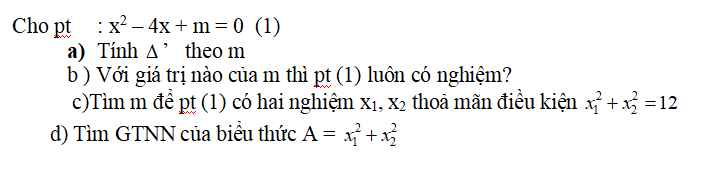 giúp mình với ạ.Mình cần lời giải chi tiết
giúp mình với ạ.Mình cần lời giải chi tiết
