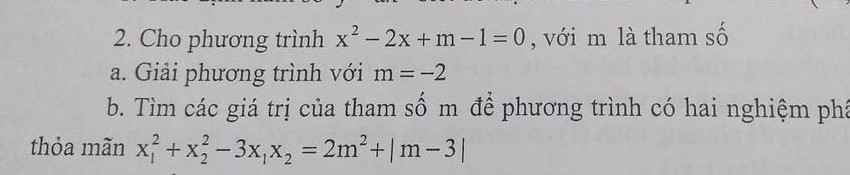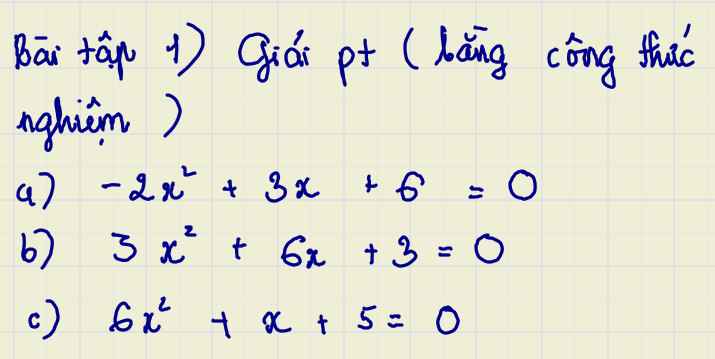a) xét delta phẩy ta có b'2 - ac
<=> 4 - m
b) để pt 1 luôn có nghiệm thì delta phẩy ≥ 0
=> 4-m ≥ 0 => m ≤ 4
c) xét delta phẩy của pt (1) ta có
4 - m để pt có 2 nghiệm x1,x2 thì delta phẩy ≥ 0 => m ≤ 4
theo Vi-ét ta có:\(\left\{{}\begin{matrix}x1+x2=4\\x1x2=m\end{matrix}\right.\)
theo bài ra ta có: x12 + x22 = 12 <=> ( x1+x2 )2 - 2x1x2 = 12
<=> 16 - 2m -12 = 0 <=> 2m = 4 <=> m = 2 ( thỏa đk)
vậy m = 2 thì pt thỏa mãn điều kiện.
d) A= x12 + x22
<=> A = (x1+x2)2 - 2x1x2
<=> A = 16 - 2m ta có m ≤ 4
nên giá trị lớn nhất của m = 4
vậy giá trị nhỏ nhất của A = 16 - 2.4
GTNN của A = 8 dấu "=" xảy ra khi m = 4
a) Ta có: a = 1 ; b' = -2 ; c = m
⇒ △' = b'2 - ac = ( -2 )2 - 1 .m = 4 - m
b) Để phương trình luôn có nghiệm thì △' \(\ge\) 0
⇒ 4 - m \(\ge\) 0 ⇔ m \(\le\) 4
Vậy khi m \(\le\) 4 thì phương trình luôn có nghiệm
c) Theo câu (b) thì phương trình luôn có nghiệm khi m \(\le\) 4
Theo hệ thức Vi - ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=4\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
Do đó:
\(x_1^2+x_2^2=12\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=12\)
\(\Leftrightarrow4^2-2m=12\)
\(\Leftrightarrow4=2m\Leftrightarrow m=2\)
Vậy khi m = 2 thì phương trình (1) có 2 nghiệm x1 ; x2 thỏa mãn x12 + x22 = 12

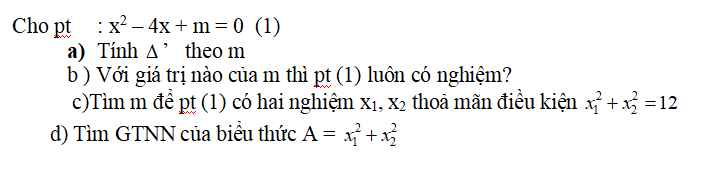 giúp mình với ạ.Mình cần lời giải chi tiết
giúp mình với ạ.Mình cần lời giải chi tiết





 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn