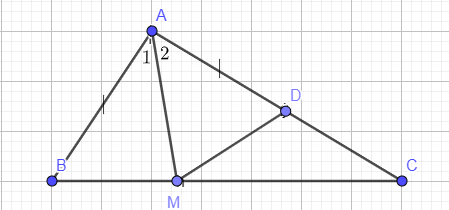
Vì `AM` là tia p/g của `\hat{BAC}=>\hat{A_1}=\hat{A_2}`
Xét `\triangle ABM` và `\triangle DAM` có:
`{:(AB=AD),(\hat{A_1}=\hat{A_2}),(\text{AM là cạnh chung}):}}=>`
`=>\triangle ABM = \triangle DAM` (c-g-c)
cho tam giác ABC có 3 góc nhọn ( AB < AC ) trên cạnh AC lấy điểm M sao cho AB = AM gọi AD là tia phân giác của góc BAC (D thuộc BC ) . từ D kẻ DI vuông góc với AB , DK vuông góc với AC ( I thuộc AB , K thuộc AC ).trên tia đối của tia AB lấy điểm P sao cho A là trung điểm của PI. CM: AD song song với PK .
Cho △ ABC nhọn có AB < AC, kẻ tia phân giác của góc BAC cắt cạnh BC tại I, trên cạnh AC lấy điểm D sao cho có AD = AB. chứng minh rằng:
a) IB = ID
b) IA là tia phân giác của góc BID
1,Cho tam giác ABC có AB < AC,AD là phân giác của góc A ( D thuộc BC ).Trên cạnh AC lấy điểm E sao cho AE = AB
a,CM:CD > BD
b,So sánh góc ADB và góc ADC
2,Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm D.Trên tia đối của tia CA lấy điểm E sao cho BD = CE.Nối D với E.Kẻ DH vuông góc với BC ( H thuộc BC ),EK vuông góc với BC ( K thuộc BC ).CM:
a,BH = CK
b,BC < DE
Cho tam giác ABC có 3 góc nhọn (AB < AC), Trên cạnh AC lấy điểm M sao cho AB = AM. Gọi AD là tia phân giác của góc BAC ( D thuộc BC)
a/ Chứng minh: △ABD = △AMD
b/ Từ D kẻ DI vuông góc với AB, DK vuông góc với AC (I thuộc AB, K thuộc AC). Chứng minh BI = KM.
Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D thuộc BC). Trên AC lấy điểm E sao cho AE = AB
a, Chứng minh rằng : Tam giác ADB tam giác ADE rồi suy ra góc ABD = gócAED
b, Tia ED cắt AB tại F. Chứng minh rằng : AC = AF
c, Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh rằng : DI = IH
1.Cho tam giác ABC có AB=AC . Kẻ tia phân giác AD của góc BAC (D thuộc BC).Trên cạnh AC lấy điểm E sao cho AE=AB, trên tia AB lấy điểm F sao cho AF=AC.Chứng minh rằng:
a)Tam giác ABE=Tam giác ACE
b)AE là đường trung trực của đoạn thẳng BC
2.Cho tam giác ABC có AB<AC .Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB, trên tia AB lấy điểm F sao cho AF=AC. Chứng minh rằng :
a)Tam giác ADF=Tam giác ACD
b)Tam giác BDF=Tam giác EDC
c)BF=AC
d)AD vuông góc FC
Cho tam giác ABC có AB < AC, tia phân giác của góc A cắt cạnh BC tại I. Trên cạnh AC lấy điểm D sao cho AD = AB
a) chứng minh rằng IA là tia phân giác của góc BID
b) Tia DI cắt tia AB tại E. Chứng minh rằng ∆IBE = ∆IDC . từ đó suy ra BD // CE
c) Chứng minh AH vuông góc với BD
d) Cho góc ABC = góc ACD. Chứng minh AB + BI = AC
Cho ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a. ∆BDF = ∆EDC
b.BF = EC
c. F, D, E thẳng hàng
d. AD ⊥ FC
Cho tam giác ABC nhọn AB< AC vẽ AD là phân giác của góc BAC D thuộc BC trên cạnh lấy điểm M sao cho AM = AB
a) Chứng minh tam giác ABD bằng tam giác ABD
b) Chứng minh tam giác BDM cân tại D
c) chứng chứng minh AD là đường trung trực của đoạn thẳng BM
