
Kiến thức áp dụng
Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
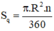

Kiến thức áp dụng
Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
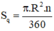
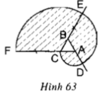
Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ (h.63).
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
b) Tính diện tích hình HOABINH (miền gạch sọc).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
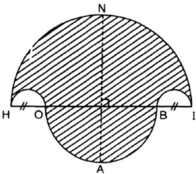
Hình 62
Trong tam giác đều ABC ,vẽ những cung tròn đi qua tâm của tam giác và từng cặp đỉnh của nó. Cho biết cạnh tam giác bằng a,tính diện tích hình hoa thị gạch sọc
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
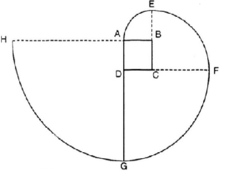
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
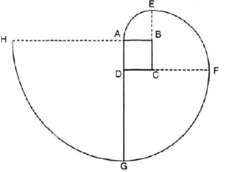
Hình 55
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
Cho hình vuông cạnh bằng a,vẽ vào phía trong hình vuông các cung tròn 900 có tâm lần lượt là các đỉnh của hình vuông,bán kính \(\dfrac{a}{2}\). Hãy cho biết diện tích của phần tạo bởi 4 cung tròn đó và hình vuông
A.a2\(\left(1-\dfrac{\pi}{2}\right)\)) B.a2\(\left(1-\dfrac{\pi}{4}\right)\) C.a2\(\left(1-\pi\right)\) D.a2-\(\dfrac{\pi}{4}\)
Cho hình vuông cạnh bằng a,vẽ vào phía trong hình vuông các cung tròn 900 có tâm lần lượt là các đỉnh của hình vuông,bán kính \(\dfrac{a}{2}\).Hãy cho biết diện tích của phần tạo bởi 4 cung tròn đó và hình vuông.
A.\(a^2\left(1-\dfrac{\pi}{2}\right)\) B.\(a^2\left(1-\dfrac{\pi}{4}\right)\) C.\(a^2\left(1-\pi\right)\) D.\(a^2-\dfrac{\pi}{4}\)
cho tam giác ABC biết các đường trung tuyến xuất phát tại các đỉnh A và B lần lượt bằng 3cm, 3,6cm; cạnh BC=4cm. tính diện tích tam giác ABC và tính hai cạnh còn lại của tam giác ABC