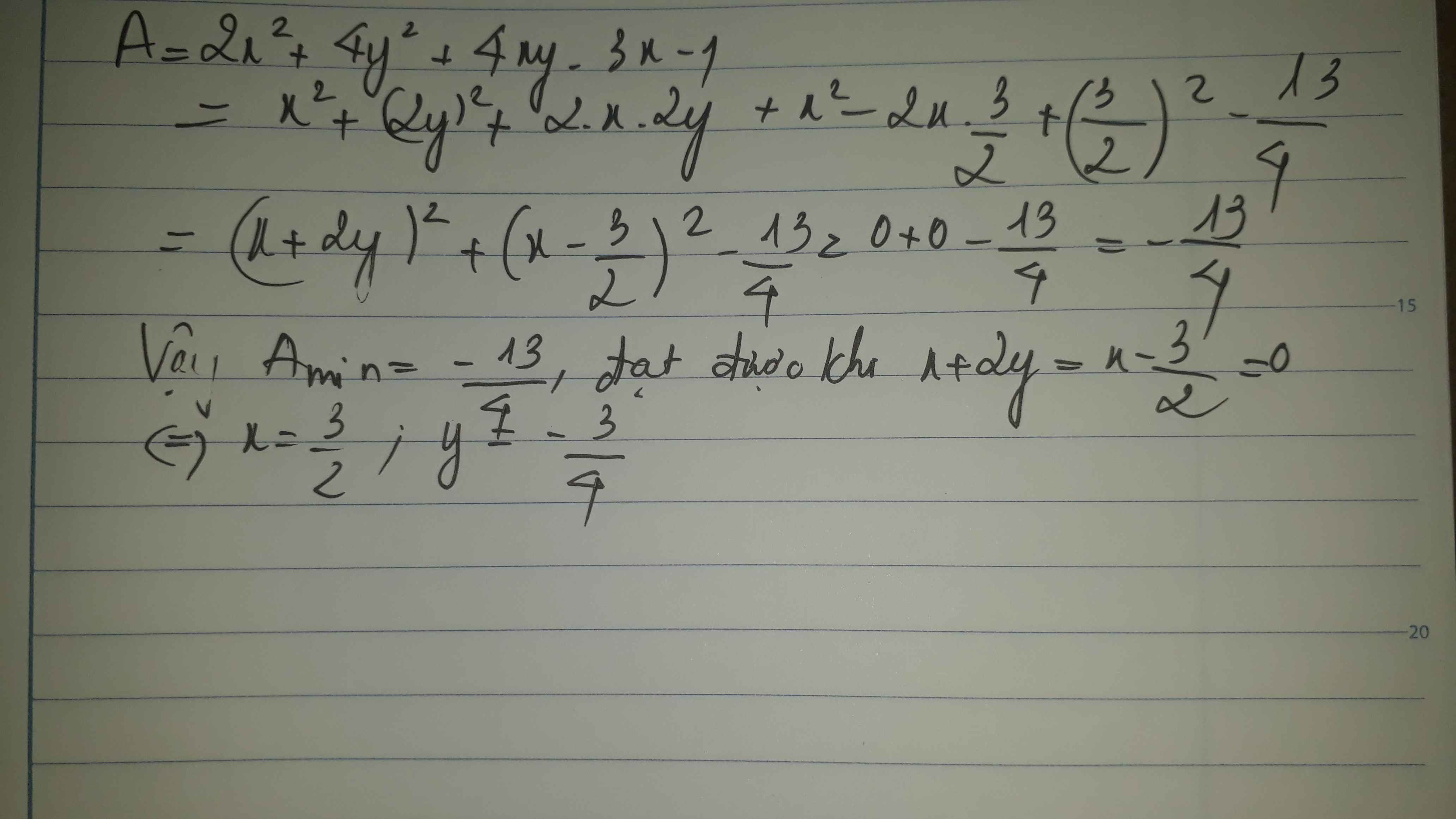\(2x^2+4y^2+4xy-3x-1\)
\(=\left(x^2+4xy+2y^2\right)+\left(x^2-3x-1\right)\)
\(=\left(x+2y\right)^2+\left(x-\dfrac{3}{2}\right)^2-\dfrac{13}{4}\)
Ta có \(\left(x+2y\right)^2+\left(x-\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+2y\right)^2+\left(x-\dfrac{3}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\forall x\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{3}{2}=0\\x+2y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-\dfrac{3}{4}\end{matrix}\right.\)
Vậy GTNN của biểu thức là \(-\dfrac{13}{4}\) khi \(x=\dfrac{3}{2}\) và \(y=-\dfrac{3}{4}\)
Ta có: \(2x^2+4y^2+4xy-3x-1\)
\(=x^2+4xy+4y^2+x^2-3x+\dfrac{9}{4}-\dfrac{13}{4}\)
\(=\left(x+2y\right)^2+\left(x-\dfrac{3}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\forall x\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-\dfrac{x}{2}=-\dfrac{3}{2}:2=\dfrac{-3}{4}\end{matrix}\right.\)