: (2,5 điểm) Cho đường tròn (O;R) và điểm A nằm ngoài (O). Qua điểm A vẽ các tiếp tuyến AM, AN (M, N là các tiếp điểm) và cát tuyến ABC của (O) (B nằm giữa A và C). Gọi H là trung điểm của BC.
a) Chứng minh tứ giác AMON nội tiếp.
b) Trong trường hợp OA=hai lần R. Hãy tính theo R diện tích hình quạt giới hạn bởi hai bán kính OM, ON và cung nhỏ MN của đường tròn (O).
c) Đường thẳng qua B song song với AN cắt đoạn thẳng MN tại K. Chứng minh hk xong xong CN
giúp mình câu c với mọi người?
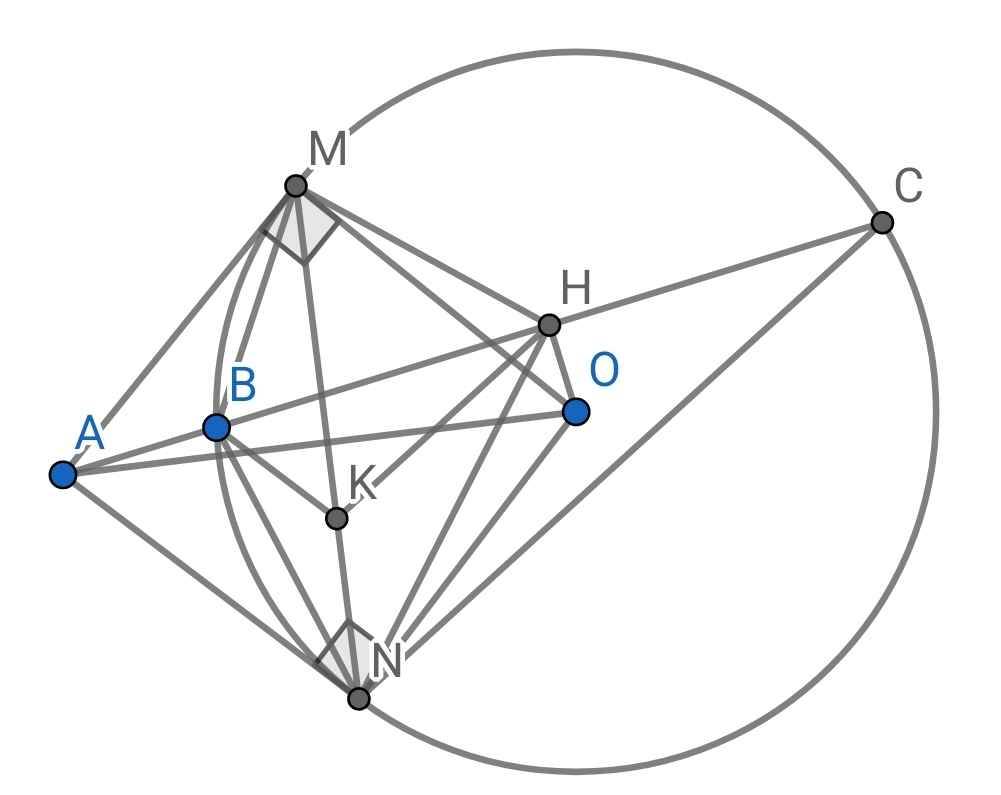
c) Do H là trung điểm của BC (gt)
⇒ OH ⊥ BC
⇒ ∆AHO vuông tại H
H thuộc đường tròn đường kính OA
⇒ A, M, H, O, N cùng thuộc đường tròn đường kính OA
Do BK // AK (gt)
⇒ ∠KBH = ∠NAH (đồng vị)
Mà ∠NAH = ∠NMH (hai góc nội tiếp cùng chắn cung KH của đường tròn đi qua năm điểm A, M, H, O, N)
⇒ ∠KBH = ∠NMH
⇒ ∠KBH = ∠KMH
⇒ B và M cùng nhìn KH dưới một góc bằng nhau
⇒ BMHN nội tiếp
⇒ ∠KHB = ∠KMB (hai góc nội tiếp cùng chắn cung BK)
Lại có:
∠KMB = ∠NCB (hai góc nội tiếp cùng chắn cung BN)
⇒ ∠KHB = ∠NCB
Mà ∠KHB và ∠NCB là hai góc đồng vị
⇒ HK // CN













