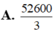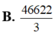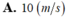\(v\left(t\right)=\int a\left(t\right)dt=\int\left(3t+4\right)dt=\dfrac{3}{2}t^2+4t+C\)
\(v\left(0\right)=4\Leftrightarrow\dfrac{3}{2}0^2+4.0+C=4\Leftrightarrow C=4\)
\(\Rightarrow v\left(t\right)=\dfrac{3}{2}t^2+4t+4\)
Quãng đường ô tô đi trong vòng \(0,5h:\)
\(s=\int\limits^{0,5}_0v\left(t\right)dt=\int\limits^{0,5}_0\left(\dfrac{3}{2}t^2+4t+4\right)dt=\left[\dfrac{1}{2}t^3+2t^2+4t\right]^{0,5}_0\)
\(\Rightarrow s=\dfrac{1}{2}.\left(\dfrac{1}{2}\right)^3+2.\left(\dfrac{1}{2}\right)^2+4.\dfrac{1}{2}=\dfrac{1}{16}+\dfrac{1}{2}+2=\dfrac{41}{16}=\dfrac{a}{b}\)
\(\Rightarrow\left\{{}\begin{matrix}a=41\\b=16\end{matrix}\right.\) \(\Rightarrow P=2a+b=2.41+16=98\)