Question

1) Cho PT : x^2 + 6x + 6m - m^2  = 0 ( với m là tham số ). Tìm m để PT đã cho có 2 nghiệm phân biệt x₁,x₂ thỏa mãn: x₁^3 - x₂^3 + 2x₁^2 + 12x₁ + 72 = 0

2) 

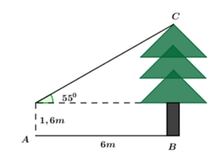
Anh Bình đứng tại vị trí A cách một đài kiểm soát không lưu 50m và nhìn thấy đỉnh C của đài này dưới một góc 55^o  so với phương nẵm ngang (như hình vẽ bên dưới).Biết khoảng cách từ mắt của anh Bình đến mặt đất bằng 1.7m . Chiều cao BC của đài kiểm soát không lưu bằng (làm tròn đến chữ số thập phân thứ hai)

Answer 1

1. Phương trình có 2 nghiệm phân biệt khi:

\(\Delta'=3^2-1\left(6m-m^2\right)>0\)

\(\Leftrightarrow m^2-6m+9>0\Leftrightarrow\left(m-3\right)^2>0\Leftrightarrow m\ne3.\)

Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-6\\x_1x_2=\dfrac{c}{a}=6m-m^2\end{matrix}\right.\) \(\left(1\right)\).

Do \(x_1\) là nghiệm của phương trình nên: \(x_1^2+6x_1+6m-m^2=0\Leftrightarrow2x_1^2+12x_1=2m^2-12m\)

Theo đề: \(\left(x_1^3-x_2^3\right)+\left(2x_1^2+12x_1\right)+72=0\)

\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)+2m^2-12m+72=0\)

\(\Leftrightarrow\left(x_1-x_2\right)\left[\left(x_1+x_2\right)^2-x_1x_2\right]+2m^2-12m+72=0\)

\(\Leftrightarrow\left(x_1-x_2\right)\left[\left(-6\right)^2-6m+m^2\right]+2\left(m^2-6m+36\right)=0\)

\(\Leftrightarrow\left(m^2-6m+36\right)\left(x_1-x_2+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}m^2-6m+36=0\\x_1-x_2+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\in\varnothing\\x_1-x_2=-2\left(2\right)\end{matrix}\right.\).

Từ \(\left(1\right),\left(2\right)\Rightarrow\left[{}\begin{matrix}m=4\\m=2\end{matrix}\right.\left(N\right)\).

Vậy: \(m\in\left\{2;4\right\}.\)