Question

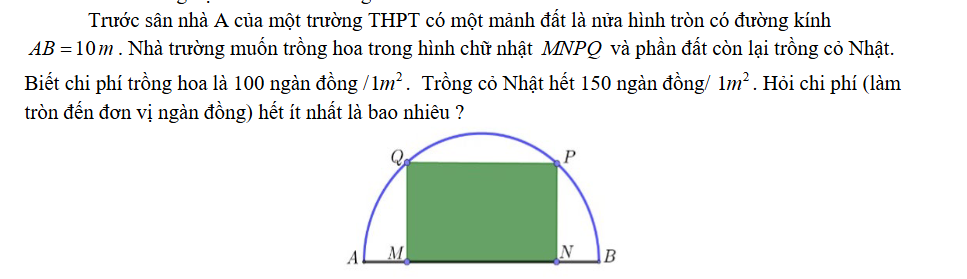
Trước sân nhà A của một trường THPT có một mảnh đất là nửa hình tròn có đường kính \( AB = 10m \). Nhà trường muốn trồng hoa trong hình chữ nhật \( MNPQ \) và phần đất còn lại trồng cỏ Nhật. Biết chi phí trồng hoa là 100 ngàn đồng / \( 1m^2 \). Trồng cỏ Nhật hết 150 ngàn đồng/ \( 1m^2 \). Hỏi chi phí (làm tròn đến đơn vị ngàn đồng) hết ít nhất là bao nhiêu ?

Answer 1

Answer 2

Bán kính \(r=\dfrac{AB}{2}=5\left(m\right)\)

Diện tích nửa hình tròn \(S=\dfrac{1}{2}\pi r^2=\dfrac{25\pi}{2}\left(m^2\right)\)

Đặt \(MN=x\left(0< x< 10\right);MQ-y\)

\(MNPQ\) là hình chữ nhật nội tiếp nửa đường tròn, ta có:

\(OM=\dfrac{x}{2};OQ=y\)

Áp dụng Pitago cho tam giác vuông \(OMQ:\dfrac{x^2}{4}+y^2=25\)

\(\Rightarrow y=\sqrt{25-\dfrac{x^2}{4}}\)

\(S_{MNPQ}=xy=x\sqrt{25-\dfrac{x^2}{4}}\left(m^2\right)\)

\(S_{cỏ}=\dfrac{25\pi}{2}-xy\)

Tổng chi phí: 

\(C=C_{hoa}+C_{cỏ}=100000xy+150000\left[\dfrac{25\pi}{2}-xy\right]=1875000\pi-50000xy\)

Để \(C_{min}\Rightarrow xy\left(max\right)\)

Áp dụng bất đẳng thức Cauchuy cho \(\dfrac{x^2}{4};25-\dfrac{x^2}{4}\)

\(\dfrac{x^2}{4}+\left(25-\dfrac{x^2}{4}\right)\ge2\sqrt{\dfrac{x^2}{4}.\left(25-\dfrac{x^2}{4}\right)}\)

\(\Rightarrow25\ge x\sqrt{25-\dfrac{x^2}{4}}=xy\)

Dấu"=" xảy ra khi \(\dfrac{x^2}{4}=25-\dfrac{x^2}{4}\Rightarrow x=5\sqrt{2}\)

\(\Rightarrow y=\sqrt{25-\dfrac{50}{4}}=\dfrac{5\sqrt{2}}{2}\)

\(\Rightarrow xy=5\sqrt{2}.\dfrac{5\sqrt{2}}{2}=25\)

\(\Rightarrow C_{min}=1875000\pi-50000xy\approx4637500\approx4638000\left(đồng\right)\)