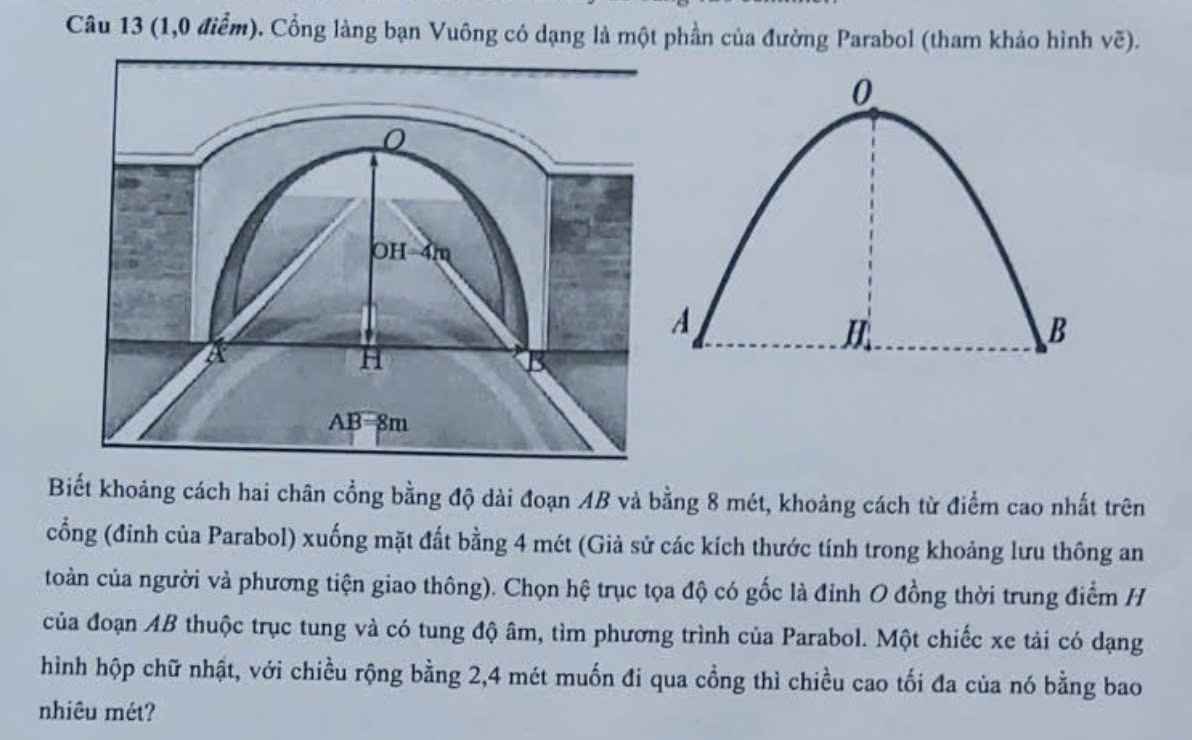
Câu 13 (1,0 điểm). Cổng làng bạn Vuông có dạng là một phần của đường Parabol (tham khảo hình vẽ).
Biết khoảng cách hai chân cổng bằng độ dài đoạn \(AB\) và bằng 8 mét, khoảng cách từ điểm cao nhất trên cổng (đỉnh của Parabol) xuống mặt đất bằng 4 mét (Giả sử các kích thước tính trong khoảng lưu thông an toàn của người và phương tiện giao thông). Chọn hệ trục tọa độ có gốc là đỉnh \(O\) đồng thời trung điểm \(H\) của đoạn \(AB\) thuộc trục tung và có tung độ âm, tìm phương trình của Parabol. Một chiếc xe tải có dạng hình hộp chữ nhật, với chiều rộng bằng 2,4 mét muốn đi qua cổng thì chiều cao tối đa của nó bằng bao nhiêu mét?
Gọi phương trình parabol là: y = ax2 + bx + c
Theo đề ta có:
(+) Khi x = 0 thì y = 0 (1)
(+) Khi x = 4 thì y = -4 (2)
(+) đỉnh của parabol có hoành độ là 0 (3)
Từ (1), (2) và (3), ta có hệ phương trình:
\(\left\{{}\begin{matrix}c=0\\16a+4b+c=-4\\-\dfrac{b}{2a}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{4}\\b=0\\c=0\end{matrix}\right.\)
Vậy parabol có phương trình: \(y=-\dfrac{1}{4}x^2\)
Thay x = 1,2 vào parabol, ta được y = -0,36
Vậy để một chiếc ô tô có chiều rộng bằng 2,4m đi qua cổng thì chiều cao tối đa là: 4 + 0,36 = 4,36 m














