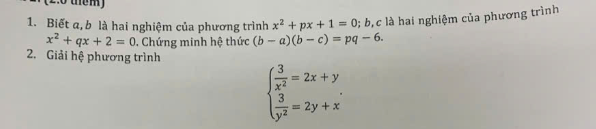Question

1. Biết \( a, b \) là hai nghiệm của phương trình \( x^2 + px + 1 = 0 \); \( b, c \) là hai nghiệm của phương trình \( x^2 + qx + 2 = 0 \). Chứng minh hệ thức \( (b-a)(b-c) = pq - 6 \).

2. Giải hệ phương trình

\[
\begin{cases}
\frac{3}{x^2} = 2x + y \\
\frac{3}{y^2} = 2y + x
\end{cases}
\]

Answer 1

2:

ĐKXĐ: x<>0; y<>0

Ta có: \(\frac{3}{x^2}=2x+y;\frac{3}{y^2}=x+2y\)

=>\(\frac{3}{x^2}-\frac{3}{y^2}=2x+y-x-2y\)

=>\(3\cdot\frac{y^2-x^2}{x^2y^2}=x-y\)

=>\(-3\cdot\frac{\left(x-y\right)\left(x+y\right)}{\left(xy\right)^2}=x-y\)

=>\(\frac{3\left(x-y\right)\left(x+y\right)}{x^2y^2}+\left(x-y\right)=0\)

=>\(\left(x-y\right)\left(\frac{3x+3y}{x^2y^2}+1\right)=0\)

TH1: x-y=0

=>x=y

\(\frac{3}{x^2}=2x+y\)

=>\(\frac{3}{x^2}=2x+x=3x\)

=>\(\frac{1}{x^2}=x\)

=>\(x^3=1\)

=>x=1

=>y=x=1

TH2: \(\frac{3x+3y}{x^2y^2}+1=0\)

=>\(\frac{3\left(x+y\right)}{x^2y^2}=-1\)

=>\(3\left(x+y\right)=-x^2y^2<0\forall x,y\)

Ta có: \(2x+y=\frac{3}{x^2};y+2x=\frac{3}{y^2}\)

=>\(2x+y+2y+x=\frac{3}{x^2}+\frac{3}{y^2}\)

=>\(3x+3y=3\left(\frac{1}{x^2}+\frac{1}{y^2}\right)>0\forall x,y\)

mà 3x+3y<0

nên (x;y)∈∅

Vậy: x=1;y=1

1: Vì a,b là các nghiệm của phương trình \(x^2+px+1=0\) nên theo Vi-et, ta có: \(a+b=-p;ab=1\)

Vì b,c là hai nghiệm của phương trình \(x^2+qx+2=0\) nên theo Vi-et, ta có: \(b+c=-q;bc=2\)

\(\left(b-a\right)\left(b-c\right)=b^2-bc-ab+ac\)

\(=b^2+bc+ab+ac-2bc-2ab\)

\(=b\left(b+c\right)+a\left(b+c\right)-2b\left(a+c\right)\)

=(b+a)(b+c)-2ba-2bc

=(-p)*(-q)-2*1-2*2

=pq-6