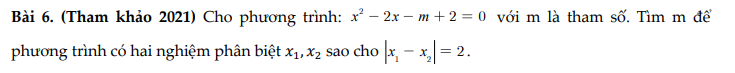\(x^2-2x-m+2=0\left(1\right)\)
Để \(\left(1\right)\) có \(2\) nghiệm phân biệt \(x_1;x_2\) khi và chỉ khi
\(\Leftrightarrow\Delta'=1+m-2>0\)
\(\Leftrightarrow m>1\)
Ta lại có \(\left|x_1-x_2\right|=2\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=4\)
\(\Leftrightarrow x_1^2+x_2^2-2x_1x_2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-4=0\)
\(\Leftrightarrow4+4\left(m-2\right)-4=0\)
\(\Leftrightarrow4m-8=0\)
\(\Leftrightarrow m=2\) thỏa \(m>1\)
Vậy với \(m=2\) thỏa mãn đề bài
Đúng 1
Bình luận (0)
