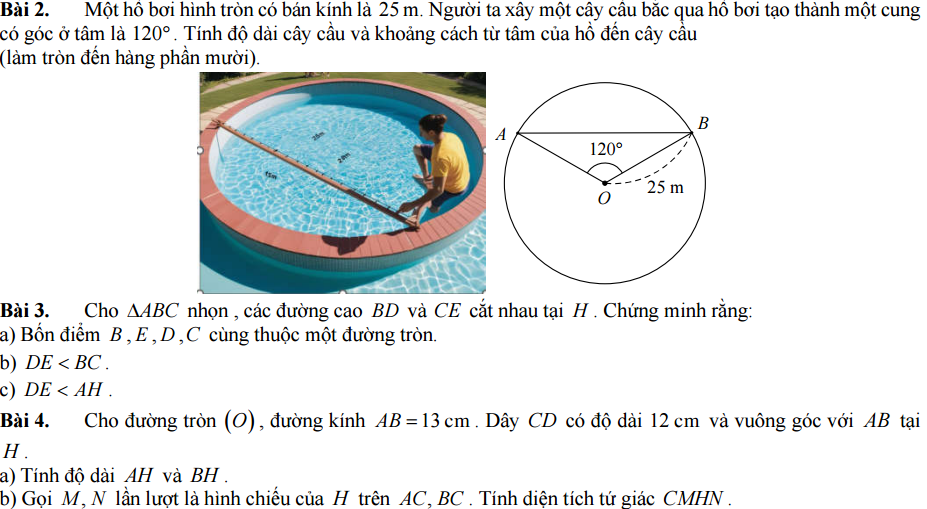
2.
Từ O kẻ \(OH\perp AB\Rightarrow H\) là trung điểm AB
\(OA=OB=25\Rightarrow\Delta OAB\) cân tại O \(\Rightarrow OH\) đồng thời là phân giác \(\widehat{AOB}\)
\(\Rightarrow\widehat{AOH}=\widehat{BOH}=\dfrac{1}{2}.120^0=60^0\)
Trong tam giác vuông AOH:
\(sin\widehat{AOH}=\dfrac{AH}{OA}\Rightarrow AH=OA.sin\widehat{AOH}=25.sin60^0=\dfrac{25\sqrt{3}}{2}\)
\(\Rightarrow AB=2AH=25\sqrt{3}\left(m\right)=43,3\left(m\right)\)
\(OH=\sqrt{OA^2-AH^2}=\sqrt{25^2-\left(\dfrac{25\sqrt{3}}{2}\right)^2}=12,5\left(m\right)\)
Bài 3:
a: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp đường tròn đường kính BC
=>B,E,D,C cùng thuộc đường tròn tâm O, với O là trung điểm của BC
b: Xét (O) có
BC là đường kính
DE là dây
Do đó: DE<BC
c: Gọi I là trung điểm của AH
Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
nên ADHE là tứ giác nội tiếp đường tròn đường kính AH
=>ADHE nội tiếp đường tròn tâm I, đường kính AH
Xét (I) có
AH là đường kính
DE là dây
Do đó: DE<AH