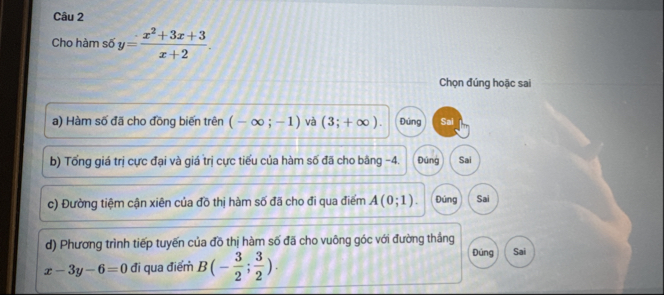
\(y'=\dfrac{\left(2x+3\right)\left(x+2\right)-\left(x^2+3x+3\right)}{\left(x+2\right)^2}=\dfrac{x^2+4x+3}{\left(x+2\right)^2}\)
\(y'=0\Rightarrow x=\left\{-3;-1\right\}\)
a. Sai
Hàm đồng biến trên \(\left(-\infty;-3\right)\) và \(\left(-1;+\infty\right)\)
b. Sai
\(y\left(-1\right)+y\left(-3\right)=1+\left(-3\right)=-2\)
c. Đúng
\(y=\dfrac{x^2+3x+2+1}{x+2}=\dfrac{\left(x+1\right)\left(x+2\right)+1}{x+2}=x+1+\dfrac{1}{x+2}\)
Nên \(y=x+1\) là TCX
Thay tọa độ A vào pt TCX thỏa mãn
d. Đúng, có 2 tiếp tuyến thỏa mãn, và 1 trong 2 tiếp tuyến đi qua B
\(x-3y-6=0\Leftrightarrow y=\dfrac{1}{3}x-2\)
Tiếp tuyến vuông góc đường thẳng trên có hệ số góc k thỏa mãn:
\(k.\left(\dfrac{1}{3}\right)=-1\Rightarrow k=-3\)
\(\dfrac{x^2+4x+3}{\left(x+2\right)^2}=-3\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\Rightarrow y=-\dfrac{7}{2}\\x=-\dfrac{3}{2}\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)