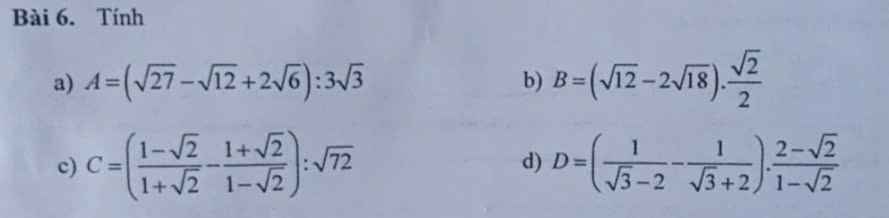a: \(A=\dfrac{\left(\sqrt{27}-\sqrt{12}+2\sqrt{6}\right)}{3\sqrt{3}}\)
\(=\dfrac{3\sqrt{3}-2\sqrt{3}+2\sqrt{6}}{3\sqrt{3}}=\dfrac{\sqrt{3}+2\sqrt{6}}{3\sqrt{3}}=\dfrac{1+2\sqrt{2}}{3}\)
b:
\(B=\left(\sqrt{12}-2\sqrt{18}\right)\cdot\dfrac{\sqrt{2}}{2}\)
\(=\left(2\sqrt{3}-2\cdot3\sqrt{2}\right)\cdot\dfrac{\sqrt{2}}{2}\)
\(=2\sqrt{3}\cdot\dfrac{\sqrt{2}}{2}-6\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=\sqrt{6}-6\)
c: \(C=\left(\dfrac{1-\sqrt{2}}{1+\sqrt{2}}-\dfrac{1+\sqrt{2}}{1-\sqrt{2}}\right):\sqrt{72}\)
\(=\dfrac{\left(1-\sqrt{2}\right)^2-\left(1+\sqrt{2}\right)^2}{\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)}:6\sqrt{2}\)
\(=\dfrac{3-2\sqrt{2}-3-2\sqrt{2}}{1-2}\cdot\dfrac{1}{6\sqrt{2}}\)
\(=\dfrac{-4\sqrt{2}}{-1}\cdot\dfrac{1}{6\sqrt{2}}=\dfrac{4\sqrt{2}}{6\sqrt{2}}=\dfrac{4}{6}=\dfrac{2}{3}\)
d: \(D=\left(\dfrac{1}{\sqrt{3}-2}-\dfrac{1}{\sqrt{3}+2}\right)\cdot\dfrac{2-\sqrt{2}}{1-\sqrt{2}}\)
\(=\dfrac{\sqrt{3}+2-\left(\sqrt{3}-2\right)}{3-4}\cdot\dfrac{-\sqrt{2}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}\)
\(=\dfrac{\sqrt{3}+2-\sqrt{3}+2}{-1}\cdot\left(-\sqrt{2}\right)\)
\(=4\sqrt{2}\)