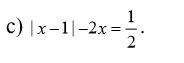\(\left|x-1\right|-2x=\dfrac{1}{2}\)
=>\(\left|x-1\right|=2x+\dfrac{1}{2}\)
=>\(\left\{{}\begin{matrix}2x+\dfrac{1}{2}>=0\\\left(2x+\dfrac{1}{2}\right)^2=\left(x-1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x>=-\dfrac{1}{2}\\\left(2x+\dfrac{1}{2}-x+1\right)\left(2x+\dfrac{1}{2}+x-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{4}\\\left(x+\dfrac{3}{2}\right)\left(3x-\dfrac{1}{2}\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{1}{4}\\x\in\left\{-\dfrac{3}{2};\dfrac{1}{6}\right\}\end{matrix}\right.\)
=>\(x=\dfrac{1}{6}\)
`c)|x-1|-2x=1/2`
`TH1:x>1=>x-1>0=>|x-1|=x-1`
Pt trở thành:
`(x-1)-2x=1/2`
`<=>x-1-2x=1/2`
`<=>-x-1=1/2`
`<=>x=-1-1/2`
`<=>x=-3/2(ktm)`
`TH2:x<=1=>x-1<=0=>|x-1|=-(x-1)`
Pt trở thành:
`-(x-1)-2x=1/2`
`<=>-x+1-2x=1/2`
`<=>-3x+1=1/2`
`<=>3x=1-1/2=1/2`
`<=>x=1/6(tm)`