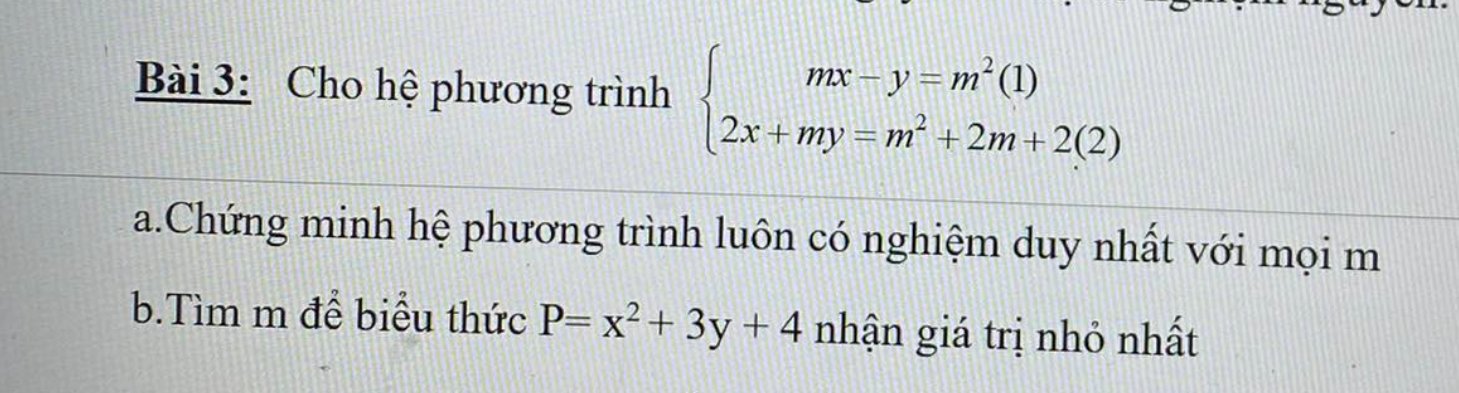a) \(\left\{{}\begin{matrix}mx-y=m^2\\2x+my=m^2+2m+2\end{matrix}\right.\)
\(D=m^2+2>0\Leftrightarrow D\ne0\)
\(\Rightarrow Hpt\) có nghiệm duy nhất \(\forall m\)
b) \(D_x=m^3+m^2+2m+2\)
\(D_y=m\left(m+2m+2\right)^2-2m^2=m^3+2m\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{D_x}{D}=\dfrac{m^3+m^2+2m+2}{m^2+2}=\dfrac{\left(m+1\right)\left(m^2+2\right)}{m^2+2}=m+1\\y=\dfrac{D_y}{D}=\dfrac{m^3+2m}{m^2+2}=\dfrac{m\left(m^2+2\right)}{m^2+2}=m\end{matrix}\right.\)
\(P=x^2+3y+4\)
\(\Leftrightarrow P=\left(m+1\right)^2+3m+4\)
\(\Leftrightarrow P=m^2+5m+5\)
\(\Leftrightarrow P=m^2+5m+\dfrac{25}{4}-\dfrac{25}{4}+5\)
\(\Leftrightarrow P=\left(m+\dfrac{5}{2}\right)^2-\dfrac{5}{4}\ge-\dfrac{5}{4},\forall m\in R\)
\(\Rightarrow GTNN\left(P\right)=-\dfrac{5}{4}\left(tại.x=-\dfrac{5}{2}\right)\)