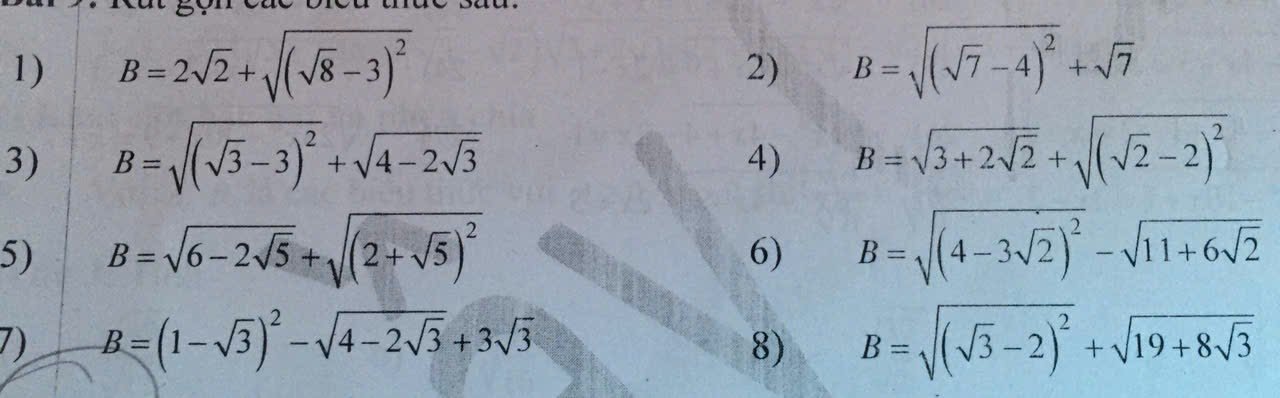\(1,B=2\sqrt{2}+\sqrt{\left(\sqrt{8}-3\right)^2}\\ =2\sqrt{2}+\left|\sqrt{8}-3\right|\\ =2\sqrt{2}+3-2\sqrt{2}\\ =3\\ 2,B=\sqrt{\left(\sqrt{7}-4\right)^2}+\sqrt{7}\\ =\left|\sqrt{7}-4\right|+\sqrt{7}\\ =4-\sqrt{7}+\sqrt{7}\\ =4\\ 3,B=\sqrt{\left(\sqrt{3}-3\right)^2}+\sqrt{4-2\sqrt{3}}\\ =\left|\sqrt{3}-3\right|+\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot1+1^2}\\ =3-\sqrt{3}+\sqrt{\left(\sqrt{3}+1\right)^2}\\ =3-\sqrt{3}+\sqrt{3}+1\\ =4\\ 4,B=\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}\\ =\sqrt{\left(\sqrt{2}\right)^2+2\cdot\sqrt{2}\cdot1+1^2}+\left|\sqrt{2}-2\right|\\ =\sqrt{\left(\sqrt{2}+1\right)^2}+2-\sqrt{2}\\=\sqrt{2}+1+2-\sqrt{2}\\ =3\)
`5)` \(B=\sqrt{6-2\sqrt{5}}+\sqrt{\left(2+\sqrt{5}\right)^2}\)
\(B=\sqrt{\left(\sqrt{5}-1\right)^2}+\left|2+\sqrt{5}\right|\)
\(B=\left|\sqrt{5}-1\right|+2+\sqrt{5}\)
\(B=\sqrt{5}-1+2+\sqrt{5}\)
\(B=2\sqrt{5}+1\)
`6)` \(B=\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{11+6\sqrt{2}}\)
\(B=\left|4-3\sqrt{2}\right|-\sqrt{\left(3+\sqrt{2}\right)^2}\)
\(B=3\sqrt{2}-4-\left|3+\sqrt{2}\right|\)
\(B=3\sqrt{2}-4-3\sqrt{2}\)
\(B=2\sqrt{2}-7\)