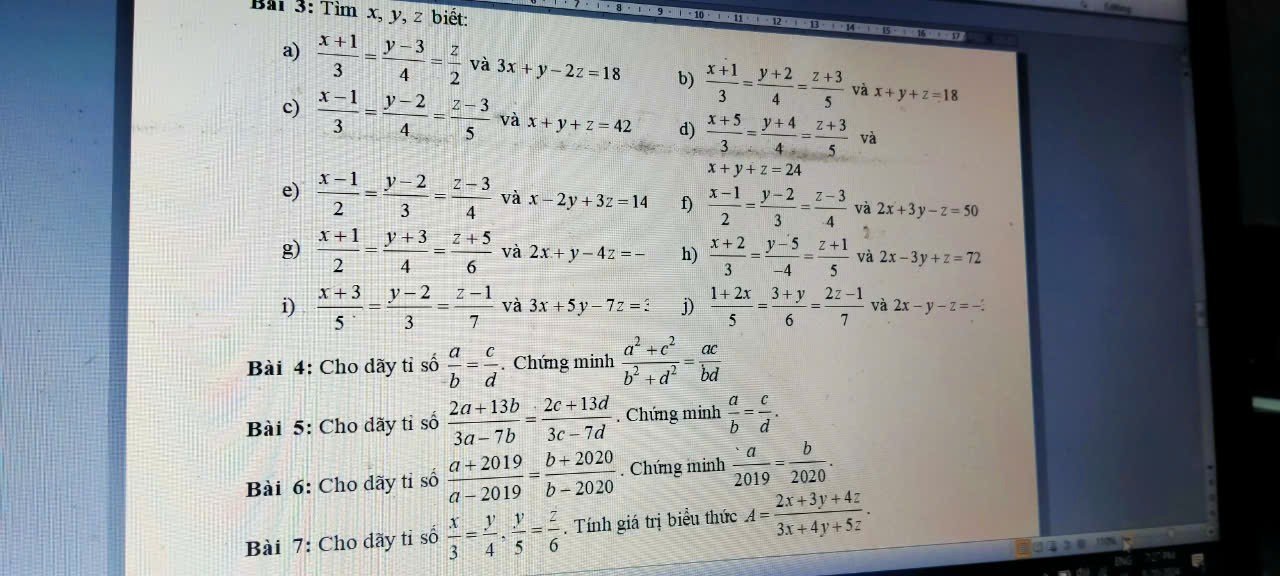
\(a)\dfrac{x+1}{3}=\dfrac{y-3}{4}=\dfrac{z}{2};3x+y-2z=18\)
Theo TCDSTLBN :
\(\dfrac{x+1}{3}=\dfrac{y-3}{4}=\dfrac{z}{2}=\dfrac{3\left(x+1\right)+\left(y-3\right)-2z}{3.3+1.4-2.2}=\dfrac{3x+y-2z}{9}=\dfrac{18}{9}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x+1}{3}=2\\\dfrac{y-3}{4}=2\\\dfrac{z}{2}=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=11\\z=4\end{matrix}\right.\)
\(b)\dfrac{x+1}{3}=\dfrac{y+2}{4}=\dfrac{z+3}{5};x+y+z=18\)
Theo TCDSTLBN :
\(\dfrac{x+1}{3}=\dfrac{y+2}{4}=\dfrac{z+3}{5}=\dfrac{x+1+y+2+z+3}{3+4+5}=\dfrac{x+y+z+6}{12}=\dfrac{18+6}{12}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x+1}{3}=2\\\dfrac{y+2}{4}=2\\\dfrac{z+3}{5}=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=6\\z=7\end{matrix}\right.\)
Bài 6:
\(\dfrac{a+2019}{a-2019}=\dfrac{b+2020}{b-2020}\)
=>\(\left(a+2019\right)\left(b-2020\right)=\left(a-2019\right)\left(b+2020\right)\)
=>\(ab-2020a+2019b-2019\cdot2020=ab+2020a-2019b-2019\cdot2020\)
=>-4040a=-4038b
=>2020a=2019b
=>\(\dfrac{a}{2019}=\dfrac{b}{2020}\)
Bài 7:
\(\dfrac{x}{3}=\dfrac{y}{4}\)
=>\(\dfrac{x}{15}=\dfrac{y}{20}\)
\(\dfrac{y}{5}=\dfrac{z}{6}\)
=>\(\dfrac{y}{20}=\dfrac{z}{24}\)
=>\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{24}=k\)
=>x=15k; y=20k; z=24k
\(A=\dfrac{2x+3y+4z}{3x+4y+5z}\)
\(=\dfrac{2\cdot15k+3\cdot20k+4\cdot24k}{3\cdot15k+4\cdot20k+5\cdot24k}\)
\(=\dfrac{30+60+96}{45+80+120}=\dfrac{186}{245}\)