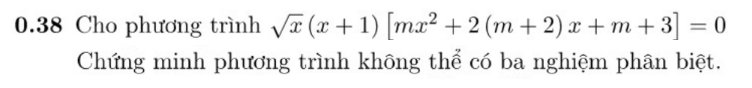`sqrt{x} (x + 1) [mx^2 + 2(m+2) x + m+3] = 0`
<=> \(\left[{}\begin{matrix}\text{ }mx^2+2\left(m+2\right)x+m+3=0\\x=0\\x=-1\end{matrix}\right.\)
Phương trình trên đã có 2 nghiệm phân biệt, chỉ cần chứng minh phương trình: `mx^2 + 2(m+2) x + m + 3 = 0` vô nghiệm
Xét `m = 0`, phương trình trở thành: `4x + 3 = 0 <=> x = -4/3` có thêm `1` nghiệm phân biệt khác (Chỉ cần đến đây là kết luận được rồi)
Xét `m ne 0`, thì phương trình có `Δ' = m + 4 < 0 <=> m < -4 `
Để ptvn thì `m < -4`, nên không thể chứng minh `ycbt`
Đúng 1
Bình luận (0)
