Áp dụng định lý Pythagore cho tam giác AHB ta có:
\(BH^2+AH^2=AB^2\\ =>AH=\sqrt{AB^2-BH^2}=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác ABC ta có:
\(AH^2=BH\cdot CH=>CH=\dfrac{AH^2}{BH}=\dfrac{\left(3\sqrt{3}\right)^2}{3}=9\left(cm\right)\)
\(AB^2=BC\cdot BH=>BC=\dfrac{AB^2}{BH}=\dfrac{6^2}{3}=12\left(cm\right)\\ AC^2=BC\cdot CH=>AC^2=BC\cdot CH=>AC=\sqrt{BC\cdot CH}=\sqrt{12\cdot9}=6\sqrt{3}\left(cm\right)\)
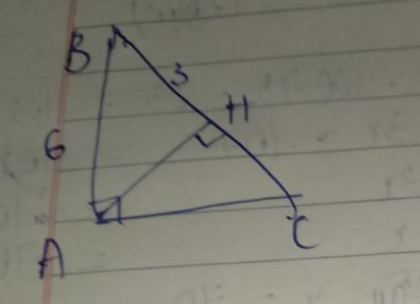
\(\Delta ABH\perp H\)
Áp dụng định lý Pythagore cho tam giác ABH ta có:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow6^2=3^2+AH^2\)
\(\Rightarrow AH=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
\(\Delta ABC\perp A\)
Áp dụng định lý Pythagore cho tam giác ABC ta có:
\(AB^2=BH.BC\)
\(\Leftrightarrow6^2=3.BC\)
\(\Rightarrow BC=6^2:3=12\left(cm\right)\)
\(BC^2=AB^2+AC^2\) (áp dụng pythagore)
\(\Leftrightarrow12^2=6^2+AC^2\)
\(\Rightarrow AC=\sqrt{12^2-6^2}=6\sqrt{3}\left(cm\right)\)
\(\Rightarrow CH=BC-BH=12-3=9\left(cm\right)\)
















