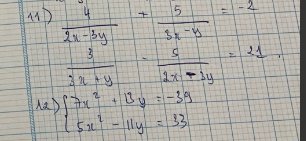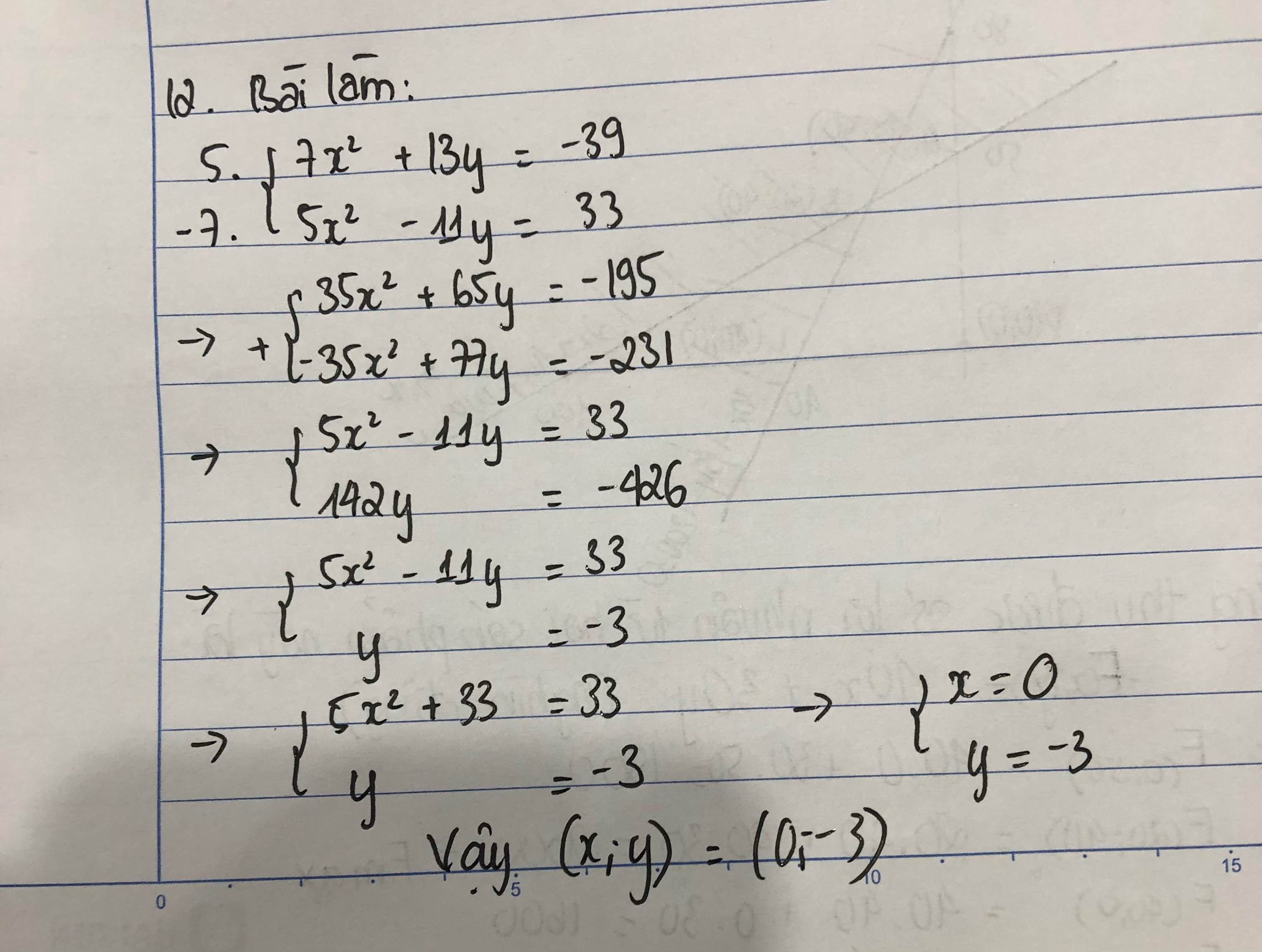11: ĐKXĐ: \(y\ne\dfrac{2}{3}x;y\ne3x\)
\(\left\{{}\begin{matrix}\dfrac{4}{2x-3y}+\dfrac{5}{3x-y}=-2\\-\dfrac{5}{2x-3y}+\dfrac{3}{3x-y}=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{20}{2x-3y}+\dfrac{25}{3x-y}=-10\\-\dfrac{20}{2x-3y}+\dfrac{12}{3x-y}=84\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{37}{3x-y}=74\\\dfrac{4}{2x-3y}+\dfrac{5}{3x-y}=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-y=\dfrac{1}{2}\\\dfrac{4}{2x-3y}=-2-\dfrac{5}{3x-y}=-2-5:\dfrac{1}{2}=-2-10=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-y=\dfrac{1}{2}\\2x-3y=-\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x-3y=\dfrac{3}{2}\\2x-3y=-\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x-3y-2x+3y=\dfrac{3}{2}+\dfrac{1}{3}\\3x-y=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=\dfrac{11}{6}\\y=3x-\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{11}{42}\\y=3\cdot\dfrac{11}{42}-\dfrac{1}{2}=\dfrac{11}{14}-\dfrac{1}{2}=\dfrac{11}{14}-\dfrac{7}{14}=\dfrac{4}{14}=\dfrac{2}{7}\end{matrix}\right.\left(nhận\right)\)