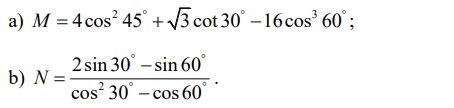a: \(M=4\cdot cos^245^0+\sqrt{3}\cdot cot30^0-16\cdot cos^360^0\)
\(=4\cdot\left(\dfrac{1}{\sqrt{2}}\right)^2+\sqrt{3}\cdot\sqrt{3}-16\cdot\left(\dfrac{1}{2}\right)^3\)
\(=4\cdot\dfrac{1}{2}+3-16\cdot\dfrac{1}{8}=8+3-2=9\)
b: \(N=\dfrac{2\cdot sin30^0-sin60^0}{cos^230^0-cos60^0}=\dfrac{2\cdot\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}}{\left(\dfrac{\sqrt{3}}{2}\right)^2-\dfrac{1}{2}}\)
\(=\dfrac{1-\dfrac{\sqrt{3}}{2}}{\dfrac{3}{4}-\dfrac{1}{2}}=\dfrac{2-\sqrt{3}}{2}:\dfrac{1}{4}=\dfrac{2-\sqrt{3}}{2}\cdot4=2\left(2-\sqrt{3}\right)\)
Đúng 1
Bình luận (0)
