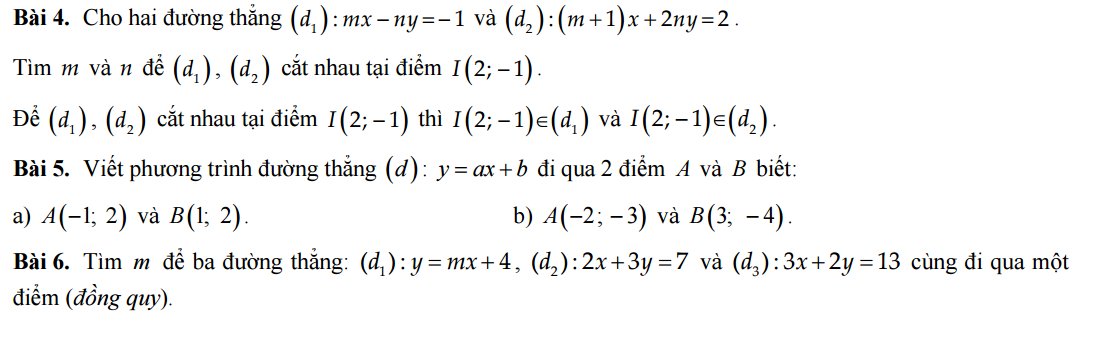Bài 4: Thay x=2 và y=-1 vào (d1), ta được:
\(m\cdot2-n\left(-1\right)=-1\)
=>2m+n=-1
Thay x=2 và y=-1 vào (d2), ta được:
\(\left(m+1\right)\cdot2+2n\cdot\left(-1\right)=2\)
=>2m+2-2n=2
=>2m-2n=0
=>m-n=0
=>n=m
2m+n=-1
=>2n+n=-1
=>3n=-1
=>\(n=-\dfrac{1}{3}\)
=>\(m=n=-\dfrac{1}{3}\)
Bài 5:
a: Thay x=-1 và y=2 vào (d), ta được:
\(a\cdot\left(-1\right)+b=2\)
=>-a+b=2(1)
Thay x=1 và y=2 vào (d), ta được:
\(a\cdot1+b=2\)
=>a+b=2(2)
Từ (1),(2) ta có hệ phương trình: \(\left\{{}\begin{matrix}-a+b=2\\a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a+b+a+b=2+2\\a+b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2b=4\\a=2-b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=2-2=0\end{matrix}\right.\)
Vậy: y=b=2
b: Thay x=-2 và y=-3 vào y=ax+b, ta được:
\(a\cdot\left(-2\right)+b=-3\)
=>-2a+b=-3(1)
Thay x=3 và y=-4 vào y=ax+b, ta được:
3a+b=-4(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2a+b=-3\\3a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+b-3a-b=-3+4\\3a+b=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-5a=1\\b=-3a-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{5}\\b=\dfrac{3}{5}-4=\dfrac{3}{5}-\dfrac{20}{5}=-\dfrac{17}{5}\end{matrix}\right.\)
Vậy: (d): \(y=-\dfrac{1}{5}x-\dfrac{17}{5}\)
Bài 6:
Tọa độ giao điểm của (d2) và (d3) là:
\(\left\{{}\begin{matrix}2x+3y=7\\3x+2y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=21\\6x+4y=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x+9y-6x-4y=21-26\\2x+3y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=-5\\2x=7-3y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-1\\x=\dfrac{7-3y}{2}=\dfrac{7-3\cdot\left(-1\right)}{2}=\dfrac{7+3}{2}=5\end{matrix}\right.\)
Thay x=5 và y=-1 vào (d1), ta được:
5m+4=-1
=>5m=-5
=>m=-1