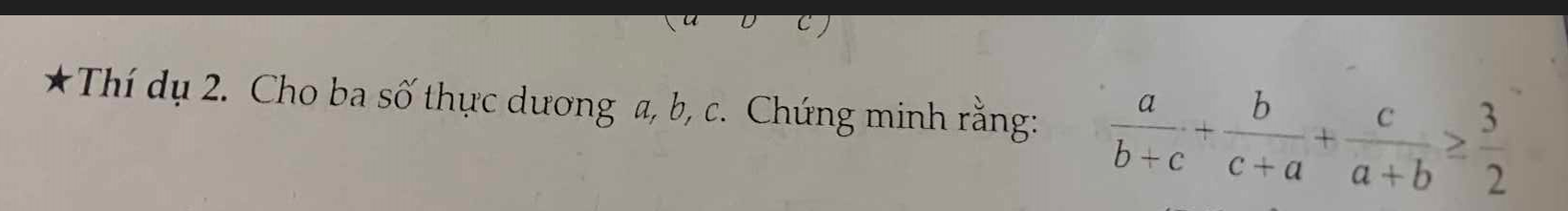VD2:
Đặt \(A=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\)
=>\(A=\left(\frac{a}{b+c}+1\right)+\left(\frac{b}{a+c}+1\right)+\left(\frac{c}{a+b}+1\right)-3\)
=>\(A=\frac{a+b+c}{a+b}+\frac{a+b+c}{a+c}+\frac{a+b+c}{b+c}-3\)
=>\(A=\left(a+b+c\right)\left(\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}\right)-3\)
\(=\frac12\left\lbrack2a+2b+2c\right\rbrack\left(\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}\right)-3\)
\(=\frac12\left\lbrack\left(a+b\right)+\left(b+c\right)+\left(a+c\right)\right\rbrack\left\lbrack\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}\right\rbrack-3\)
Theo Cosi, ta có:
\(\left\lbrack\left(a+b\right)+\left(b+c\right)+\left(a+c\right)\right\rbrack\cdot\left\lbrack\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}\right\rbrack\ge3\cdot\sqrt[3]{\left(a+b\right)\left(b+c\right)\left(a+c\right)}\cdot3\cdot\sqrt[3]{\frac{1}{\left(a+b\right)\left(a+c\right)\left(b+c\right)}}\)
=>\(\left\lbrack\left(a+b\right)+\left(b+c\right)+\left(a+c\right)\right\rbrack\cdot\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\right)\ge9\)
=>\(\frac12\left\lbrack\left(a+b\right)+\left(b+c\right)+\left(a+c\right)\right\rbrack\cdot\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\right)\ge9\cdot\frac12=\frac92\)
=>\(A\ge\frac92-3=\frac32\)