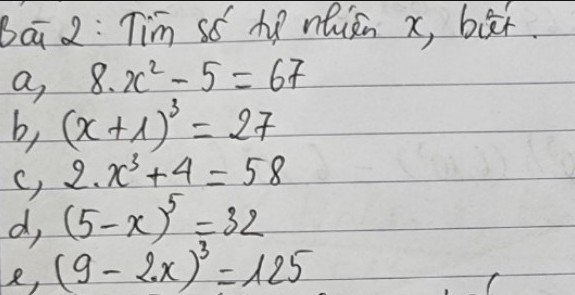a: \(8x^2-5=67\)
=>\(8x^2=5+67=72\)
=>\(x^2=\dfrac{72}{8}=9\)
=>\(\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
b: \(\left(x+1\right)^3=27\)
=>\(\left(x+1\right)^3=3^3\)
=>x+1=3
=>x=2
c; \(2x^3+4=58\)
=>\(2x^3=58-4=54\)
=>\(x^3=\dfrac{54}{2}=27=3^3\)
=>x=3
d: \(\left(5-x\right)^5=32\)
=>\(\left(5-x\right)^5=2^5\)
=>5-x=2
=>x=5-2=3
e: \(\left(9-2x\right)^3=125\)
=>\(\left(9-2x\right)^3=5^3\)
=>9-2x=5
=>2x=9-5=4
=>x=4:2=2
`8x^2-5=67`
`=> 8x^2 = 72`
`=> x^2 = 9
\(\Rightarrow x=\pm3\)
`b) (x + 1)^3 = 27`
`=> (x+1)^3 = 3^3`
`=> x+1 = 3`
`=> x = 2`
`c)2x^3 + 4 = 58`
`=> 2x^3 = 54`
`=> x^3 = 27`
`=> x^3 = 3^3`
`=> x=3`
`d)(5-x)^5 = 32`
`=> (5-x)^5 = 2^5`
`=> 5 - x = 2`
`=> x = 3`
`e)(9-2x)^3=125`
`=> (9 - 2x)^3 = 5^3`
`=> 9 - 2x = 5`
`=> 2x = 4`
`=> x = 2`