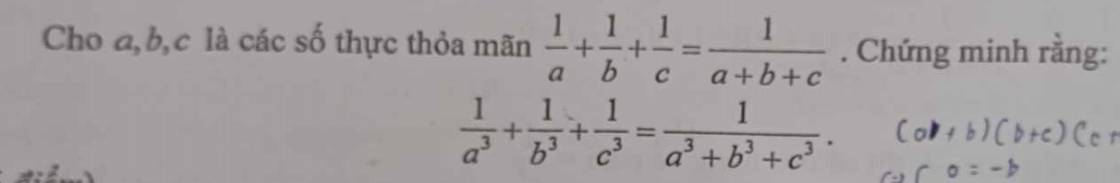Ta có: \(\frac{1}{a}+\frac1b+\frac1c=\frac{1}{a+b+c};(a,b,c\ne0)\)
\(\Leftrightarrow \frac1a+\frac1b=\frac{1}{a+b+c}-\frac1c\\\Leftrightarrow \frac{a+b}{ab}=\frac{c-a-b-c}{c(a+b+c)}\\\Leftrightarrow\frac{a+b}{ab}+\frac{a+b}{c(a+b+c)}=0\\\Leftrightarrow(a+b)\left[\frac{1}{ab}+\frac{1}{c(a+b+c)}\right]=0\\\Leftrightarrow(a+b).\frac{c(a+b+c)+ab}{abc(a+b+c)}=0\\\Rightarrow (a+b)(ca+bc+c^2+ab)=0(\text{vì }abc(a+b+c)\ne 0)\\\Leftrightarrow (a+b)[b(c+a)+c(c+a)]=0\\\Leftrightarrow(a+b)(b+c)(c+a)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=-b\\b=-c\\c=-a\end{matrix}\right.\)
+, Với \(a=-b\) thì: \(\begin{cases} \frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{1}{(-b)^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{1}{c^3}\\ \frac{1}{a^3+b^3+c^3}=\frac{1}{(-b)^3+b^3+c^3}=\frac{1}{c^3} \end{cases} \)
\(\Rightarrow \frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{1}{a^3+b^3+c^3}\)
Tương tự với các TH còn lại, ta có đpcm
$\text{#}Toru$