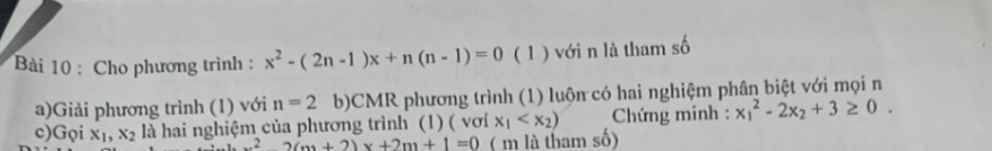a: Thay n=2 vào (1), ta được:
\(x^2-\left(2\cdot2-1\right)x+2\left(2-1\right)=0\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
b: \(\Delta=\left[-\left(2n-1\right)\right]^2-4n\left(n-1\right)\)
\(=4n^2-4n+1-4n^2+4n=1>0\)
=>Phương trình luôn có hai nghiệm phân biệt
c: Vì \(\Delta=1\)
nên phương trình (1) có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{2n-1-1}{2}=\dfrac{2n-2}{2}=n-1\\x=\dfrac{2n-1+1}{2}=\dfrac{2n}{2}=n\end{matrix}\right.\)
=>\(x_1=n-1;x_2=n\)
\(x_1^2-2x_2+3\)
\(=\left(n-1\right)^2-2n+3\)
\(=n^2-2n+1-2n+3=n^2-4n+4=\left(n-2\right)^2>=0\forall n\)
Đúng 1
Bình luận (0)
