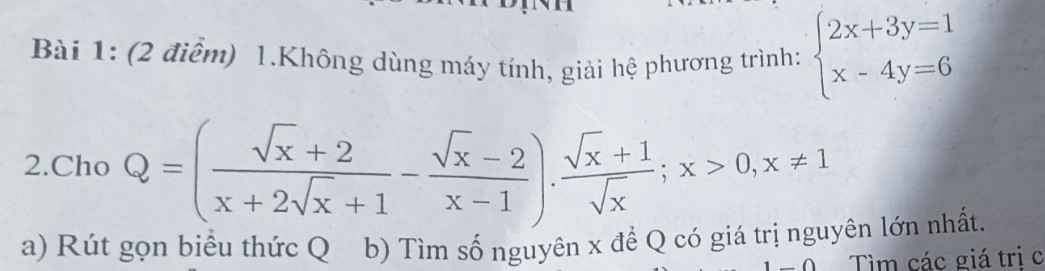1. \(\left\{{}\begin{matrix}2x+3y=1\\x-4y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=1\\2x-8y=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11y=-11\\x-4y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=2\end{matrix}\right.\).
Vậy: Hệ phương trình có nghiệm duy nhất: \(\left(x;y\right)=\left(2;-1\right)\).
2. (a) Viết lại được \(Q\) thành:
\(Q=\left[\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}\left(x-1\right)}=\dfrac{2}{x-1}\)
(b) \(Q\in Z\Rightarrow\left(x-1\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\).
Để \(Q_{max}\) thì \(\left\{{}\begin{matrix}\left(x-1\right)_{min}\\x-1>0\end{matrix}\right.\Rightarrow x-1=1\Leftrightarrow x=2\) (thỏa mãn).
Vậy: \(x=2.\)