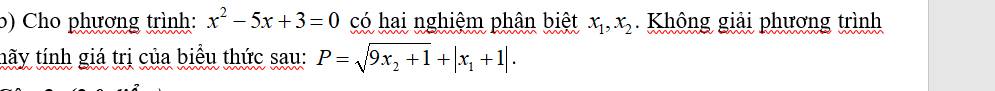Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=3\end{matrix}\right.\Rightarrow x_1,x_2>0\)
Do đó, ta có được: \(x_1=P-1-\sqrt{9x_2-1}\)
Thay vào định lí Vi-ét: \(P-1-\sqrt{9x_2-1}+x_2=5\).
\(\Leftrightarrow x_2^2+\left(2P-21\right)x_2+P^2-12P+35=0\)
Đồng nhất hệ số phương trình với \(x^2-5x+3=0\Rightarrow\left\{{}\begin{matrix}2P-21=-5\\P^2-12P+35=3\end{matrix}\right.\).
Tìm được: \(P=8.\)
Đúng 2
Bình luận (0)
